题目内容
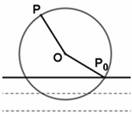
一半径为2m的水轮如图所示,水轮圆心O距离水面1m;已知水轮按逆时针做匀速转动,每3s转一圈,如果当水轮上点P从水中浮现时(图中点P0)开始计算时间.
(1)试建立适当的坐标系,将点P距离水面的高度h(m)表示为时间t(s)的函数;
(2)点P第一次到达最高点大约要多长时间?
(3)记f(t)=h,求证:不论t为何值,f (t)+f (t+1)+f (t+2)是定值.
(1)试建立适当的坐标系,将点P距离水面的高度h(m)表示为时间t(s)的函数;
(2)点P第一次到达最高点大约要多长时间?
(3)记f(t)=h,求证:不论t为何值,f (t)+f (t+1)+f (t+2)是定值.
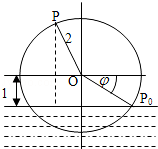
解:(1)以水轮所在平面与水面的交线为x轴,以过点O且与水面垂直的直线为y轴,建立如图所示的直角坐标系,
设h=Asin(ωt+φ)+k,(﹣ <φ<0),
<φ<0),
则A=2,k=1,
∵T=3= ,
,
∴ω=
∴h=2sin( t+φ)+1,
t+φ)+1,
∵t=0,h=0,
∴0=2sinφ+1,
∴sinφ=﹣ ,
,
∴﹣ <φ<0,
<φ<0,
∴φ=﹣ ,
,
∴h=2sin( t﹣
t﹣ )+1
)+1
(2)令2sin( t﹣
t﹣ )+1=3,
)+1=3,
得sin( t﹣
t﹣ )=1,
)=1,
∴ t﹣
t﹣ =
= ,
,
∴t=1,
∴点P第一次到达最高点大约要1s的时间;
(3)由(1)知:f (t)=2sin( t﹣
t﹣ )+1=
)+1= sin
sin t﹣cos
t﹣cos t+1,
t+1,
f (t+1)=2sin( t+
t+ )+1=2cos
)+1=2cos t+1,
t+1,
f (t+2)=2sin( t+
t+ )+1=﹣
)+1=﹣ sin
sin t﹣cos
t﹣cos t+1,
t+1,
∴f (t)+f (t+1)+f (t+2)=3(为定值).
设h=Asin(ωt+φ)+k,(﹣
 <φ<0),
<φ<0),则A=2,k=1,
∵T=3=
 ,
,∴ω=

∴h=2sin(
 t+φ)+1,
t+φ)+1,∵t=0,h=0,
∴0=2sinφ+1,
∴sinφ=﹣
 ,
,∴﹣
 <φ<0,
<φ<0,∴φ=﹣
 ,
,∴h=2sin(
 t﹣
t﹣ )+1
)+1(2)令2sin(
 t﹣
t﹣ )+1=3,
)+1=3,得sin(
 t﹣
t﹣ )=1,
)=1,∴
 t﹣
t﹣ =
= ,
,∴t=1,
∴点P第一次到达最高点大约要1s的时间;
(3)由(1)知:f (t)=2sin(
 t﹣
t﹣ )+1=
)+1= sin
sin t﹣cos
t﹣cos t+1,
t+1,f (t+1)=2sin(
 t+
t+ )+1=2cos
)+1=2cos t+1,
t+1,f (t+2)=2sin(
 t+
t+ )+1=﹣
)+1=﹣ sin
sin t﹣cos
t﹣cos t+1,
t+1,∴f (t)+f (t+1)+f (t+2)=3(为定值).


练习册系列答案
相关题目
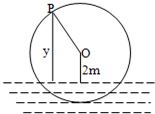 如图为一半径为3m的水轮,水轮中心O距水面2m,已知水轮每分钟旋转4圈,水轮上的点P到水面距离y(m)与时间x(t)满足函数关系y=Asin(ωx+φ)+2则( )
如图为一半径为3m的水轮,水轮中心O距水面2m,已知水轮每分钟旋转4圈,水轮上的点P到水面距离y(m)与时间x(t)满足函数关系y=Asin(ωx+φ)+2则( )A、ω=
| ||
B、ω=
| ||
C、ω=
| ||
D、ω=
|
 一半径为2m的水轮如图所示,水轮圆心O距离水面1m;已知水轮按逆时针做匀速转动,每3s转一圈,如果当水轮上点P从水中浮现时(图中点P0)开始计算时间.
一半径为2m的水轮如图所示,水轮圆心O距离水面1m;已知水轮按逆时针做匀速转动,每3s转一圈,如果当水轮上点P从水中浮现时(图中点P0)开始计算时间.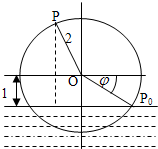 一半径为2m的水轮如图所示,水轮圆心O距离水面1m;已知水轮按逆时针做匀速转动,每3s转一圈,如果当水轮上点P从水中浮现时(图中点P0)开始计算时间.
一半径为2m的水轮如图所示,水轮圆心O距离水面1m;已知水轮按逆时针做匀速转动,每3s转一圈,如果当水轮上点P从水中浮现时(图中点P0)开始计算时间.