题目内容
18.设函数f(x)=x2-x+b,已知log2f(a)=2,且f(log2a)=b(a>0且a≠1),求a、b的值.分析 根据f(log2a)=b(a>0且a≠1),可得log2a=0,或log2a=1,进而求出a值,代入log2f(a)=2,可得b值.
解答 解:∵f(log2a)=(log2a)2-(log2a)+b=b,
故log2a=0,或log2a=1,
即a=1(舍去)或a=2,
∵log2f(a)=log2f(2)=2,
∴f(2)=22-2+b=4,
∴b=2.
点评 本题考查的知识点是二次函数的图象性质,对数运算,熟练掌握二次函数的图象和性质,是解答的关键.

练习册系列答案
相关题目
8.下列结论正确的个数是( )
①若x>0,则x>sinx恒成立;
②命题“?x>0,x-lnx>0”的否定是“?x>0,x0-lnx0≤0”;
③“命题p∨q为真”是“命题p∧q为真”的充分不必要条件.
①若x>0,则x>sinx恒成立;
②命题“?x>0,x-lnx>0”的否定是“?x>0,x0-lnx0≤0”;
③“命题p∨q为真”是“命题p∧q为真”的充分不必要条件.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
6.如图,在三棱锥V-ABC,VA=VC,VB⊥AC,则AB与BC的大小关系是( )
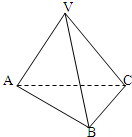

| A. | AB>BC | B. | AB=BC | C. | AB<BC | D. | 无法确定 |
13.已知函数f(x)=2cosx-$\frac{1}{x}$,若$\frac{π}{3}$<a<b<$\frac{5π}{6}$,则( )
| A. | f(a)>f(b) | B. | f(a)<f(b) | C. | f(a)=f(b) | D. | f(a)f(b)>0 |
8.若loga-1(2x-1)>loga-1(x-1),则有( )
| A. | a>1,x>0 | B. | a>1,x>1 | C. | a>2,x>0 | D. | a>2,x>1 |