题目内容
16.若函数f(x)=sin2ωπx(ω>0)的图象在区间[0,$\frac{1}{2}$]上至少有两个最高点,两个最低点,则ω的取值范围为( )| A. | ω>2 | B. | ω≥2 | C. | ω>3 | D. | ω≥3 |
分析 先求得函数f(x)=$\frac{1}{2}$-$\frac{1}{2}$cos2ωπx,根据题意可得区间[0,$\frac{1}{2}$]上至少包含$\frac{3}{2}$个周期,故有$\frac{3}{2}$•$\frac{2π}{2ωπ}$≤$\frac{1}{2}$,由此求得ω的范围.
解答 解:因为函数f(x)=sin2ωπx=$\frac{1-cos2ωπx}{2}$=$\frac{1}{2}$-$\frac{1}{2}$cos2ωπx (ω>0)的图象在区间[0,$\frac{1}{2}$]上至少有两个最高点和两个最低点,
则区间[0,$\frac{1}{2}$]上至少包含$\frac{3}{2}$个周期,故有$\frac{3}{2}$•$\frac{2π}{2ωπ}$≤$\frac{1}{2}$,求得ω≥3,
故选:D.
点评 本题主要考查二倍角公式、余弦函数的图象特征,属于基础题.

练习册系列答案
相关题目
6.函数y=$tan(2x-\frac{π}{4})$的其中一个对称中心为( )
| A. | $(-\frac{π}{8},0)$ | B. | $(\frac{π}{2},0)$ | C. | (0,0) | D. | $(\frac{π}{4},0)$ |
11.已知函数f(x)是定义在R上的奇函数,且当x>0时,f(x)=$\frac{5}{2}$cos($\frac{π}{2}$x)+log${\;}_{\frac{1}{2}}$x,则函数f(x)的零点个数为( )
| A. | 4 | B. | 6 | C. | 7 | D. | 9 |
8.下列结论正确的个数是( )
①若x>0,则x>sinx恒成立;
②命题“?x>0,x-lnx>0”的否定是“?x>0,x0-lnx0≤0”;
③“命题p∨q为真”是“命题p∧q为真”的充分不必要条件.
①若x>0,则x>sinx恒成立;
②命题“?x>0,x-lnx>0”的否定是“?x>0,x0-lnx0≤0”;
③“命题p∨q为真”是“命题p∧q为真”的充分不必要条件.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
6.如图,在三棱锥V-ABC,VA=VC,VB⊥AC,则AB与BC的大小关系是( )
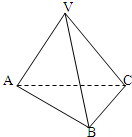

| A. | AB>BC | B. | AB=BC | C. | AB<BC | D. | 无法确定 |