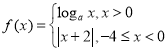题目内容
【题目】已知函数![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)当m>0时,若对于区间[1,2]上的任意两个实数x1,x2,且x1<x2,都有![]() ,成立,求m的最大值.
,成立,求m的最大值.
【答案】(1)见解析 (2)![]() .
.
【解析】
(1)先求导,再分类讨论,根据导数和函数的单调性的关系即可解决,(2)根据题意可得f(x2)-x22)<f(x1)-x12,构造函数,再求导,再分离参数,利用导数求出函数的最值即可.
(1)f(x)的定义域是(0,+∞), f′(x)=x+m+![]() =
=![]() ,
,
m≥0时,f′(x)>0, 故m≥0时,f(x)在(0,+∞)递增;
m<0时,方程x2+mx+m=0的判别式为: △=m2-4m>0,
令f′(x)>0,解得:x>![]() ,
,
令f′(x)<0,解得:0<x<![]() ,
,
故m<0时,f(x)在(![]() ,+∞)递增,在(0,
,+∞)递增,在(0,![]() )递减;
)递减;
(2)由(1)知,当m>0时,函数f(x)在(0,+∞)递增,
又[1,2]![]() (0,+∞),故f(x)在[1,2]递增;
(0,+∞),故f(x)在[1,2]递增;
对任意x1<x2,都有f(x1)<f(x2), 故f(x2)-f(x1)>0,
由题意得:f(x2)-f(x1)<![]() , 整理得:f(x2)-
, 整理得:f(x2)-![]() <f(x1)-
<f(x1)-![]() ,
,
令F(x)=f(x)-x2=-![]() x2+mx+mlnx, 则F(x)在[1,2]递减, 故F′(x)=
x2+mx+mlnx, 则F(x)在[1,2]递减, 故F′(x)=![]() ,
,
当x∈[1,2]时,-x2+mx+m≤0恒成立,即m≤![]() ,
,
令h(x)=![]() ,则h′(x)
,则h′(x)![]() >0, 故h(x)在[1,2]递增,
>0, 故h(x)在[1,2]递增,
故h(x)∈[![]() ,
,![]() ], 故m≤
], 故m≤![]() .
.
![]() 实数
实数![]() 的最大值为
的最大值为![]() .
.

练习册系列答案
 启东小题作业本系列答案
启东小题作业本系列答案
相关题目