题目内容
20.已知向量$\overrightarrow a$=(cos(x+$\frac{π}{8}$),sin2(x+$\frac{π}{8}$)),$\overrightarrow b$=(sin(x+$\frac{π}{8}$),1),函数f(x)=1-2$\overrightarrow a$•$\overrightarrow b$.(1)求f(x)的解析式和最小正周期;
(2)求f(x)的单调递减区间;
(3)若方程f(x)+2m=0在[$\frac{π}{4}$,$\frac{7π}{8}$]有两个实根,试求实数m的取值范围.
分析 (1)根据数量积的运算、二倍角公式和两角和与差的正弦、余弦公式化简f(x)的解析式,根据余弦函数的图象与性质求函数的周期;
(2)根据余弦函数的单调减区间,解不等式确定函数f(x)的单调减区间;
(3)由题意可得cos2x=-$\sqrt{2}$m在[$\frac{π}{4}$,$\frac{7π}{8}$]有两个实根,由余弦函数的图象和性质,可得-1<-$\sqrt{2}$m≤0,解不等式即可得到m的范围.
解答 解:(1)由题意得,f(x)=1-2$\overrightarrow a$•$\overrightarrow b$
=1-2[cos(x+$\frac{π}{8}$)sin(x+$\frac{π}{8}$)+sin2(x+$\frac{π}{8}$)]
=1-2cos(x+$\frac{π}{8}$)sin(x+$\frac{π}{8}$)-2sin2(x+$\frac{π}{8}$)
=sin(2x+$\frac{π}{4}$)+cos(2x+$\frac{π}{4}$)
=$\sqrt{2}$sin(2x+$\frac{π}{4}$+$\frac{π}{4}$)=$\sqrt{2}$cos2x,
最小正周期为T=$\frac{2π}{2}$=π;
(2)由2kπ≤2x≤2kπ+π,解得kπ≤x≤kπ+$\frac{π}{2}$,k∈Z,
则函数f(x)的单调递减区间是:[kπ,kπ+$\frac{π}{2}$],k∈Z;
(3)方程f(x)+2m=0在[$\frac{π}{4}$,$\frac{7π}{8}$]有两个实根,
即为cos2x=-$\sqrt{2}$m在[$\frac{π}{4}$,$\frac{7π}{8}$]有两个实根,
由t=2x∈[$\frac{π}{2}$,$\frac{7π}{4}$],y=cost在[$\frac{π}{2}$,π]递减,在[π,$\frac{7π}{4}$]递增,
即有y=cos2t的最小值为-1,最大值为$\frac{\sqrt{2}}{2}$,
即有-1<-$\sqrt{2}$m≤0,解得0≤m<$\frac{\sqrt{2}}{2}$.
故实数m的取值范围是[0,$\frac{\sqrt{2}}{2}$).
点评 本题考查数量积的运算,三角函数恒等变换公式的应用,余弦函数图象与性质,解题过程中注意运用整体的思想来解决三角函数问题.

 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案| A. | 1条 | B. | 2条 | C. | 超过2条但有限 | D. | 无数条 |
| A. | 1 | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
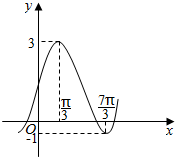 已知平面向量$\overrightarrow{a}$=(sin$\frac{ωx}{2}$cos$\frac{ωx}{2}$,cos2$\frac{ωx}{2}$),$\overrightarrow{b}$=(cosφ,sinφ),函数f(x)=2A($\overrightarrow{a}$•$\overrightarrow{b}$)-Asinφ+k(其中A>0,|φ|<$\frac{π}{2}$)的图象如图所示.
已知平面向量$\overrightarrow{a}$=(sin$\frac{ωx}{2}$cos$\frac{ωx}{2}$,cos2$\frac{ωx}{2}$),$\overrightarrow{b}$=(cosφ,sinφ),函数f(x)=2A($\overrightarrow{a}$•$\overrightarrow{b}$)-Asinφ+k(其中A>0,|φ|<$\frac{π}{2}$)的图象如图所示.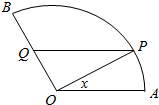 如图,准备在扇形空地AOB上修建一个山水景观OPQ,己知∠AOB=$\frac{2}{3}$π,OA=lkm,点P在扇形弧上,PQ∥OA交OB于点Q,记∠POA=x.
如图,准备在扇形空地AOB上修建一个山水景观OPQ,己知∠AOB=$\frac{2}{3}$π,OA=lkm,点P在扇形弧上,PQ∥OA交OB于点Q,记∠POA=x.