题目内容
12.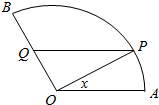 如图,准备在扇形空地AOB上修建一个山水景观OPQ,己知∠AOB=$\frac{2}{3}$π,OA=lkm,点P在扇形弧上,PQ∥OA交OB于点Q,记∠POA=x.
如图,准备在扇形空地AOB上修建一个山水景观OPQ,己知∠AOB=$\frac{2}{3}$π,OA=lkm,点P在扇形弧上,PQ∥OA交OB于点Q,记∠POA=x.(Ⅰ)当Q是OB中点时,求PQ的长;
(Ⅱ)求使山水景观OPQ的面积S最大时x的值;
(Ⅲ)为了方便路人休闲行走,要在扇形空地上铺设一条从入口A到出口B的观光道路,道路由弧$\widehat{AP}$,线段PQ以及线段QB组成,怎样设计才能使得观光道路最长?
分析 (Ⅰ)当Q是OB中点时,在△OPQ中,由余弦定理得OP2=QO2+PQ-2QO2•PQcos$\frac{π}{3}$,求PQ的长;
(Ⅱ)S=$\frac{1}{2}PQ•POsinx$,利用三角函数知识求使山水景观OPQ的面积S最大时x的值;
(Ⅲ)首先将道路长度f(x)表达成x的函数关系式,再利用导数方法研究函数的最大值,从而可以求得观光道路最长.
解答 解:(Ⅰ)当Q是OB中点时,OQ=$\frac{1}{2}$,∠PQO=$\frac{π}{3}$,OP=1,
在△OPQ中,由余弦定理得OP2=QO2+PQ-2QO2•PQcos$\frac{π}{3}$,
∴PQ=$\frac{1+\sqrt{13}}{4}$;
(Ⅱ)在△OPQ中,由正弦定理得PQ=$\frac{2\sqrt{3}}{3}$sin($\frac{2}{3}$π-x),x∈(0,$\frac{2}{3}$π),
∴S=$\frac{1}{2}PQ•POsinx$=$\frac{\sqrt{3}}{3}$sin($\frac{2}{3}$π-x)sinx=$\frac{\sqrt{3}}{6}$sin(2x-$\frac{π}{6}$)+$\frac{\sqrt{3}}{12}$,
∴sin(2x-$\frac{π}{6}$)=1,x=$\frac{π}{3}$时,山水景观OPQ的面积S最大值问为$\frac{\sqrt{3}}{4}$;
(Ⅲ)设道路长度为f(x),
△OPQ中,由正弦定理得OQ=$\frac{2\sqrt{3}}{3}$sinx,x∈(0,$\frac{1}{3}$π),
则f(x)=x+$\frac{2\sqrt{3}}{3}$sin($\frac{2}{3}$π-x)+(1-$\frac{2\sqrt{3}}{3}$sinx)=x+cosx-$\frac{\sqrt{3}}{3}$x,
由f′(x)=1-sinx-$\frac{\sqrt{3}}{3}$cosx=0得sin(x+$\frac{π}{6}$)=$\frac{\sqrt{3}}{2}$
∵x∈(0,$\frac{1}{3}$π),∴x=$\frac{π}{6}$
易得x∈(0,$\frac{π}{6}$),f′(x)>0,θ∈($\frac{π}{6}$,$\frac{π}{3}$),f′(x)<0,
∴x=$\frac{π}{6}$时,f(x)取到最大值$\frac{π}{6}$+$\frac{\sqrt{3}}{3}$+1.
点评 解决实际问题的关键在于建立数学模型和目标函数,把“问题情境”译为数学语言,找出问题的主要关系,并把问题的主要关系抽象成数学问题,在数学领域寻找适当的方法解决,再返回到实际问题中加以说明.

| A. | (-∞,-$\frac{{e}^{2}+1}{e}$) | B. | (-∞,e2) | C. | (-2e2,1-e2) | D. | (1-e2,1) |
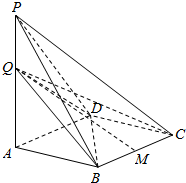 已知四棱锥P-ABCD中,底面ABCD为∠ABC=$\frac{2}{3}$π的菱形,PA⊥平面ABCD,点Q在直线PA上.
已知四棱锥P-ABCD中,底面ABCD为∠ABC=$\frac{2}{3}$π的菱形,PA⊥平面ABCD,点Q在直线PA上.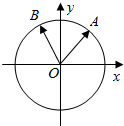 如图,在平面直角坐标系中,锐角α和钝角β的终边分别与单位圆交于A,B两点,
如图,在平面直角坐标系中,锐角α和钝角β的终边分别与单位圆交于A,B两点,