题目内容
函数y=sinx,x∈[-
,
]的值域是( )
| π |
| 6 |
| 2π |
| 3 |
| A、[-1,1] | ||||||
B、[-
| ||||||
C、[-
| ||||||
D、[
|
分析:根据正弦函数的图象即可求出函数的值域.
解答:解:作出函数y=sinx对应的图象如图: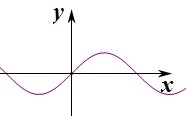
由三角函数的图象可知,当x=-
时,y取得最小值为y=sin(-
)=-
.
当x=
时,y取得最大值为y=sin
=1.
∴-
≤y≤1,
即函数的值域为[-
,1].
故选:B.

由三角函数的图象可知,当x=-
| π |
| 6 |
| π |
| 6 |
| 1 |
| 2 |
当x=
| π |
| 2 |
| π |
| 2 |
∴-
| 1 |
| 2 |
即函数的值域为[-
| 1 |
| 2 |
故选:B.
点评:本题主要考查三角函数的图象和性质,利用三角函数的图象即可求函数的值域,比较基础.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目