题目内容

19．若集合A={1，9}，B={-1，x2}，则“x=3”是“A∩B={9}”的（　　）
A．必要不充分条件B．充分不必要条件
C．充要条件D．既不充分也不必要条件

分析 根据集合的关系以及充分条件和必要条件的定义进行判断即可．

解答 解：若A∩B={9}，则x2=9，即x=3或x=-3，
则“x=3”是“A∩B={9}”的充分不必要条件，
故选：B．

点评 本题主要考查充分条件和必要条件的判断，根据集合的关系求出x的值是解决本题的关键．

练习册系列答案
相关题目
9．已知椭圆C1：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的一个顶点与抛物线C2：x2=4y的焦点重合，F1、F2分别是椭圆C1的左、右焦点，C1的离心率e=$\frac{\sqrt{2}}{2}$，过F2的直线l与椭圆C1交于M，N两点，与抛物线C2交于P，Q两点．
（1）求椭圆C1的方程；
（2）当直线l的斜率k=-1时，求△PQF1的面积；
（3）在x轴上是否存在点A，$\overrightarrow{AM}$•$\overrightarrow{AN}$为常数？若存在，求出点A的坐标和这个常数；若不存在，请说明理由．
10．已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的半焦距为c，且b=c，椭圆的上顶点到右顶点的距离为2$\sqrt{3}$．
（1）求椭圆的方程；
（2）已知点F是椭圆的右焦点，C（m，0）是线段OF上一个动点（O为坐标原点），是否存在过点F且与x轴不垂直的直线l与椭圆交于A，B两点，使得AC|=|BC|，并说明理由．
7．直线l1：（m-1）x-y+2m+1=0与圆C：（x+2）2+（y-3）2=$\sqrt{2}$的位置关系是（　　）
A．相交B．相切C．相离D．以上都有可能
14．已知f（x）=x2+ax-$\frac{b^2}{4}+1{，_{\;}}$g（x）=2x，
（1）若A={t∈N*|t2-10t+9≤0}，当a，b∈A时，求f（x）＞g（x）恒成立的概率；
（2）若B=[0，9]，当a，b∈B时，求f（x）＞g（x）恒成立的概率．
4．已知定点F1（-$\sqrt{3}$，0），F2（$\sqrt{3}$，0）曲线C是使得|RF1|+|RF2|为定值（大于|F1F2|）的点R的轨迹，且曲线C过点T（0，1）．
（1）求曲线C的方程；
（2）若直线l过点F2，且与曲线C交于P，Q两点，当△F1PQ的面积取得最大值时，求直线l的方程．
11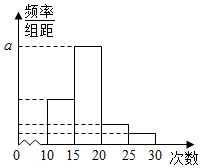．对某校高一年级学生参加社区服务次数进行统计，随机抽取M名学生作为样本，得到这M名学生参加社区服务的次数．根据此数据作出了频数与频率的统计表和频率分布直方图如下：
分组频数频率
[10，15）100.25
[15，20）25n
[20，25）mp
[25，30）20.05
合计M1
（1）求出表中M、p及图中a的值；
（2）试估计他们参加社区服务的平均次数；
（3）在所取样本中，从参加社区服务的次数不少于20次的学生中任选2人，求至少1人参加社区服务次数在区间[20，25）内的概率．
8．下列叙述中，是随机变量的有（　　）
①某工厂加工的零件，实际尺寸与规定尺寸之差；②标准状态下，水沸腾的温度；③某大桥一天经过的车辆数；④向平面上投掷一点，此点坐标．
A．②③B．①②C．①③④D．①③
9．函数f（x）=ax3+bx2+cx+d在x=0处的切线方程为8x+y-1=0，且函数f（x）在x=-2和x=4处有极值．
（1）求函数f（x）的解析式；
（2）求函数f（x）在x∈[-3，3]的最大值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网