题目内容
8.已知函数$f(x)=\frac{1-x}{e^x}$(1)求函数f(x)的极值
(2)若x∈[-1,+∞),求函数f(x)的最值.
分析 (1)求出函数的对数,解关于导函数的不等式,求出函数的极值即可;(2)根据函数的单调性,求出函数的最值即可.
解答 解:(1)f′(x)=$\frac{x-2}{{e}^{x}}$,
令f′(x)>0,解得:x>2,
令f′(x)<0,解得:x<2,
故f(x)在(-∞,2)递减,在(2,+∞)递增,
故f(x)的极小值是f(2)=-$\frac{1}{{e}^{2}}$;无极大值;
(2)由(1)f(x)在[-1,2)递减,在(2,+∞)递增,
而f(-1)=$\frac{2}{{e}^{-1}}$=2e>f(2)=-$\frac{1}{{e}^{2}}$,
故f(x)有最小值-$\frac{1}{{e}^{2}}$,无最大值.
点评 本题考查了函数的单调性、极值、最值问题,考查导数的应用,是一道中档题.

练习册系列答案
相关题目
16.若a,b∈R,且ab>0,则$\frac{b}{a}$+$\frac{a}{b}$的最小值是( )
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 2$\sqrt{2}$ |
20.已知棱长为$\sqrt{3}$的正方体ABCD-A1B1C1D1内部有一圆柱,此圆柱恰好以直线AC1为轴,则该圆柱侧面积的最大值为( )
| A. | $\frac{{9\sqrt{2}}}{8}π$ | B. | $\frac{{9\sqrt{2}}}{4}π$ | C. | $2\sqrt{3}π$ | D. | $3\sqrt{2}π$ |
 如图,在正三棱柱ABC-A1B1C1中,AB=4,AA1=6,E,F分别为BB1,AC的中点.
如图,在正三棱柱ABC-A1B1C1中,AB=4,AA1=6,E,F分别为BB1,AC的中点.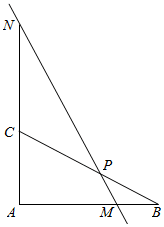 如图,Rt△ABC中,P是斜边BC上一点,且满足:$\overrightarrow{BP}=\frac{1}{2}\overrightarrow{PC}$,点M,N在过点P的直线上,若$\overrightarrow{AM}=λ\overrightarrow{AB},\overrightarrow{AN}=μ\overrightarrow{AC}$,(λ,μ>0),则λ+2μ的最小值为( )
如图,Rt△ABC中,P是斜边BC上一点,且满足:$\overrightarrow{BP}=\frac{1}{2}\overrightarrow{PC}$,点M,N在过点P的直线上,若$\overrightarrow{AM}=λ\overrightarrow{AB},\overrightarrow{AN}=μ\overrightarrow{AC}$,(λ,μ>0),则λ+2μ的最小值为( )