题目内容
已知A(3,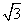 ),O是原点,点P(x,y)的坐标满足
),O是原点,点P(x,y)的坐标满足 的取值范围为________.
的取值范围为________.
[-3,3]
[解析] 作出可行域如图,

所以 cosθ=2
cosθ=2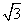 cosθ∈[-3,3].
cosθ∈[-3,3].

练习册系列答案
 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
题目内容
已知A(3,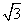 ),O是原点,点P(x,y)的坐标满足
),O是原点,点P(x,y)的坐标满足 的取值范围为________.
的取值范围为________.
[-3,3]
[解析] 作出可行域如图,

所以 cosθ=2
cosθ=2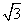 cosθ∈[-3,3].
cosθ∈[-3,3].

 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案