题目内容
17.已知函数f(x)=alnx+x2(a为实数).(Ⅰ)求函数f(x)在区间[1,e]上的最小值及相应的x值;
(Ⅱ)若存在x∈[1,e],使得f(x)≤(a+2)x成立,求实数a的取值范围.
分析 (Ⅰ)先求出导函数f'(x),然后讨论a研究函数在[1,e]上的单调性,将f(x)的各极值与其端点的函数值比较,其中最小的一个就是最小值;
(Ⅱ)若存在x∈[1,e],f(x)≤(a+2)x成立,即a(x-lnx)≥x2-2x,构造函数g(x)=$\frac{{{x^2}-2x}}{x-lnx}$(x∈[1,e]),可将问题转化为一个函数成立问题,由此求出函数的最小值,即可得到结论.
解答 (Ⅰ)解:f(x)=alnx+x2的定义域为(0,+∞),
f′(x)=$\frac{a}{x}$+2x=$\frac{{2{x^2}+a}}{x}$,
当x∈[1,e]时,2x2∈[2,2e2],
若a≥-2,f′(x)在[1,e]上非负(仅当a=-2,x=-1时,f′(x)=0),
故f(x)在[1,e]上单调递增,此时f(x)min=f(1)=1;
若-2e2<a<-2,令f′(x)<0,解得1≤x<$\sqrt{\frac{-a}{2}}$,此时f(x)单调递减;
令f′(x)>0,解得$\sqrt{\frac{-a}{2}}$<x≤e,此时f(x)单调递增,
∴f(x)min=f($\sqrt{\frac{-a}{2}}$)=$\frac{a}{2}ln(\frac{-a}{2})-\frac{a}{2}$;
若a≤-2e2,f′(x)在[1,e]上非正(仅当a=-2e2,x=e时,f′(x)=0),
故f(x)在[1,e]上单调递减,此时f(x)min=f(e)=a+e2,
综上所述,得a≥-2时,f(x)min=1,相应的x=1;
当-2e2<a<-2时,f(x)min=$\frac{a}{2}ln(\frac{-a}{2})-\frac{a}{2}$,相应的x=$\sqrt{\frac{-a}{2}}$;
当a≤-2e2时,f(x)min=a+e2,相应的x=e;
(Ⅱ)解:不等式f(x)≤(a+2)x可化为a(x-lnx)≥x2-2x.
∵x∈[1,e],∴lnx≤1≤x且等号不能同时成立,∴lnx<x,即x-lnx>0,
因而a≥$\frac{{{x^2}-2x}}{x-lnx}$,x∈[1,e],令g(x)=$\frac{{{x^2}-2x}}{x-lnx}$(x∈[1,e]),
则g′(x)=$\frac{(x-1)(x+2-2lnx)}{{{{(x-lnx)}^2}}}$,
当x∈[1,e]时,x-1≥0,lnx≤1,x+2-2lnx>0,
从而g′(x)≥0(仅当x=1时取等号),∴g(x)在[1,e]上是增函数,
故g(x)min=g(1)=-1,
∴实数a的取值范围是[-1,+∞).
点评 本题主要考查了利用导数研究函数的单调性,以及利用导数求闭区间上函数的最值,同时考查不等式存在性问题的解法,属于中档题.

 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
| A. | $\frac{4}{41}$ | B. | $\frac{4}{5}$ | C. | $\frac{4}{25}$ | D. | $\frac{4\sqrt{41}}{41}$ |
| A. | (-∞,3]∪[4,+∞) | B. | [3,4] | C. | (-∞,3] | D. | [4,+∞) |
| A. | -8 | B. | 8 | C. | 5 | D. | 15 |
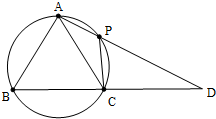 在△ABC中,AB=AC,过点A的直线与其外接圆交于点P,交BC延长线于点D.
在△ABC中,AB=AC,过点A的直线与其外接圆交于点P,交BC延长线于点D.