题目内容
7.已知函数f(x)=sin2x-|sinx|-|cosx|(x∈R),则f(x)的值域为[-1-$\sqrt{2}$,1-$\sqrt{2}$].分析 设|sinx|+|cosx|=t,两边平方即可得到|sin2x|=t2-1,从而可求出t的范围$[1,\sqrt{2}]$,讨论sin2x>0时,得到函数t2-t-1,根据该二次函数的单调性即可求出该函数在$[1,\sqrt{2}]$上的取值范围,即求出了f(x)此时的范围,同理可求出sin2x<0时f(x)的取值范围,这两个取值范围求并集即得f(x)的值域.
解答 解:设|sinx|+|cosx|=t,则:
|sinx|2+|2sinxcosx|+|cosx|2=t2;
∴|sin2x|=t2-1;
∴0≤t2-1≤1,t>0;
∴$1≤t≤\sqrt{2}$;
①当sin2x>0时,将原函数变成关于t的函数g(t)=t2-t-1;
g(t)在$[1,\sqrt{2}]$上单调递增;
∴$g(1)≤g(t)≤g(\sqrt{2})$;
∴$-1≤g(t)≤1-\sqrt{2}$;
②当sin2x<0时,将原函数变成关于t的函数h(t)=-t2-t+1;
h(t)在$[1,\sqrt{2}]$上单调递减;
∴$h(\sqrt{2})≤h(t)≤h(1)$;
∴$-1-\sqrt{2}≤h(t)≤-1$;
∴综上得f(x)的值域为[$-1-\sqrt{2}$,$1-\sqrt{2}$].
故答案为:$[-1-\sqrt{2},1-\sqrt{2}]$.
点评 考查二倍角的正弦公式,sin2x+cos2x=1,以及换元求函数值域的方法,二次函数的单调性,根据二次函数的单调性求函数值域.

练习册系列答案
相关题目
18.已知抛物线y2=4x,过其焦点F作倾斜角为$\frac{π}{4}$的直线l,若l与抛物线交于B、C两点,则弦BC的长为( )
| A. | $\frac{10}{3}$ | B. | 2 | C. | 4 | D. | 8 |
15.执行如图所示的程序框图,输出的结果是( )
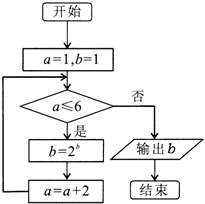

| A. | 4 | B. | 8 | C. | 16 | D. | 216 |
2.将函数y=f(x)的图象向右平移$\frac{π}{2}$个单位得到函数y=cos2x的图象,再将函数y=f(x)的横坐标伸长到原来的2倍,纵坐标不变,得到函数y=g(x)的图象,则g(x)=( )
| A. | -sin4x | B. | cos4x | C. | sinx | D. | -cosx |
12.复数z=$\frac{2i}{i-1}$+i3(i为虚数单位)的共轭复数为( )
| A. | 1+2i | B. | i-1 | C. | 1-i | D. | 1-2i |
16.某几何体的三视图如图所示,且正视图、侧视图都是矩形,则该几何体的体积是( ) 

| A. | 16 | B. | 12 | C. | 8 | D. | 6 |
 如图:在三棱锥P-ABC中,AB=AC=2$\sqrt{10}$,BC=4,PC=2$\sqrt{11}$,点P在平面ABC内的射影恰为△ABC的重心G,M为侧棱AP上一动点.
如图:在三棱锥P-ABC中,AB=AC=2$\sqrt{10}$,BC=4,PC=2$\sqrt{11}$,点P在平面ABC内的射影恰为△ABC的重心G,M为侧棱AP上一动点.