题目内容
6.已知极坐标系的极点与直角坐标系的原点重合,极轴与x轴的非负半轴重合,长度单位相同,直线l的参数方程为:$\left\{\begin{array}{l}x=t-1\\ y=t+1\end{array}\right.({t为参数})$,曲线C的极坐标方程为:ρ=2$\sqrt{2}$sin(θ-$\frac{π}{4}}$).(Ⅰ)判断曲线C的形状,简述理由;
(Ⅱ)设直线l与曲线C相交于M,N,O是坐标原点,求三角形MON的面积.
分析 (Ⅰ)运用两角差的正弦公式和ρ2=x2+y2,x=ρcosθ,y=ρsinθ,即可得到曲线C的普通方程,即可判断形状;
(Ⅱ)将直线l的参数方程代入圆的普通方程,可得M,N的坐标,再由三角形的面积公式计算即可得到.
解答 解:(Ⅰ)ρ=2$\sqrt{2}$sin(θ-$\frac{π}{4}}$)即为ρ=2$\sqrt{2}$($\frac{\sqrt{2}}{2}$sinθ-$\frac{\sqrt{2}}{2}$cosθ)
=2sinθ-2cosθ,即ρ2=2ρsinθ-2ρcosθ,
即有x2+y2+2x-2y=0,即为(x+1)2+(y-1)2=2,
则曲线C的形状为以(-1,1)为圆心,$\sqrt{2}$为半径的圆;
(Ⅱ)将直线l的参数方程为:$\left\{\begin{array}{l}x=t-1\\ y=t+1\end{array}\right.({t为参数})$,
代入圆(x+1)2+(y-1)2=2,可得2t2=2,
解得t=±1,
可得M(0,2),N(-2,0),
则三角形MON的面积为S=$\frac{1}{2}$×2×2=2.
点评 本题考查极坐标方程和普通方程的互化,同时考查直线和圆的位置关系,考查运算能力,属于基础题.

练习册系列答案
相关题目
18.已知抛物线y2=4x,过其焦点F作倾斜角为$\frac{π}{4}$的直线l,若l与抛物线交于B、C两点,则弦BC的长为( )
| A. | $\frac{10}{3}$ | B. | 2 | C. | 4 | D. | 8 |
15.执行如图所示的程序框图,输出的结果是( )
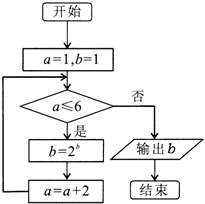

| A. | 4 | B. | 8 | C. | 16 | D. | 216 |
16.某几何体的三视图如图所示,且正视图、侧视图都是矩形,则该几何体的体积是( ) 

| A. | 16 | B. | 12 | C. | 8 | D. | 6 |
 如图,三棱柱ABC-A1B1C1中,侧面BCC1B1是矩形,截面A1BC是等边三角形.
如图,三棱柱ABC-A1B1C1中,侧面BCC1B1是矩形,截面A1BC是等边三角形.  如图,四棱锥P-ABCD的底面ABCD是平行四边形,M,N分别为PB,CD的中点,二面角P-CD-A的大小为60°,AC=AD=$\sqrt{2}$,CD=PN=2,PC=PD.
如图,四棱锥P-ABCD的底面ABCD是平行四边形,M,N分别为PB,CD的中点,二面角P-CD-A的大小为60°,AC=AD=$\sqrt{2}$,CD=PN=2,PC=PD.