题目内容
5.设△ABC的内角A,B,C所对边的长分别为a,b,c,若a=1,c=4$\sqrt{2}$且△ABC的面积为2,则sinC=( )| A. | $\frac{4}{41}$ | B. | $\frac{4}{5}$ | C. | $\frac{4}{25}$ | D. | $\frac{4\sqrt{41}}{41}$ |
分析 S△ABC=$\frac{1}{2}acsinB$=2,可得sinB=$\frac{\sqrt{2}}{2}$.利用余弦定理可得:b2=a2+c2-2accosB=25或41,b=5或$\sqrt{41}$,利用正弦定理可得:$\frac{b}{sinB}=\frac{c}{sinC}$,代入解出即可.
解答 解:∵S△ABC=$\frac{1}{2}acsinB$=$\frac{1}{2}×1×4\sqrt{2}×sinB$=2,∴sinB=$\frac{\sqrt{2}}{2}$.
∴b2=a2+c2-2accosB=$1+(4\sqrt{2})^{2}$-2×$1×4\sqrt{2}$×$(±\frac{\sqrt{2}}{2})$=25或41,
∴b=5或$\sqrt{41}$,
∴b=5.
由正弦定理可得:$\frac{b}{sinB}=\frac{c}{sinC}$,
∴sinC=$\frac{4\sqrt{2}×\frac{\sqrt{2}}{2}}{5}$=$\frac{4}{5}$.
同理b=$\sqrt{41}$时,sinC=$\frac{4\sqrt{41}}{41}$.
故选:无答案.
点评 本题考查了正弦定理余弦定理、三角形的面积计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
15.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的左、右焦点分别为F1、F2,过F1作圆x2+y2=a2的切线分别交双曲线的左、右两支于点B、C,且|BC|=|CF2|,则双曲线的渐近线方程为( )
| A. | y=±3x | B. | y=±2$\sqrt{2}$x | C. | y=±($\sqrt{3}$+1)x | D. | y=±($\sqrt{3}$-1)x |
15.执行如图所示的程序框图,输出的结果是( )
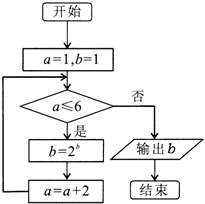

| A. | 4 | B. | 8 | C. | 16 | D. | 216 |
 如图,三棱柱ABC-A1B1C1中,侧面BCC1B1是矩形,截面A1BC是等边三角形.
如图,三棱柱ABC-A1B1C1中,侧面BCC1B1是矩形,截面A1BC是等边三角形.  如图,四棱锥P-ABCD的底面ABCD是平行四边形,M,N分别为PB,CD的中点,二面角P-CD-A的大小为60°,AC=AD=$\sqrt{2}$,CD=PN=2,PC=PD.
如图,四棱锥P-ABCD的底面ABCD是平行四边形,M,N分别为PB,CD的中点,二面角P-CD-A的大小为60°,AC=AD=$\sqrt{2}$,CD=PN=2,PC=PD.