题目内容
已知函数f(x)=x2+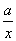 (x≠0,常数a∈R)
(x≠0,常数a∈R)
(1)讨论函数f(x)的奇偶性,并说明理由;
(2)若函数f(x)在x∈[2,+∞)上为增函数,求实数a的取值范围.
解析 (1)函数f(x)的定义域为{x|x≠0},
当a=0时,f(x)=x2,(x≠0)
显然为偶函数;当a≠0时,f(1)=1+a,f(-1)=1-a,
因此f(1)≠f(-1),且f(-1)≠-f(1),
所以函数f(x)=x2+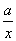 既不是奇函数,也不是偶函数.
既不是奇函数,也不是偶函数.
(2)f′(x)=2x- =
= ,
,
当a≤0,f′(x)>0,则f(x)在(2,+∞)上是增函数,
当a>0时,由f′(x)= >0,解得x>
>0,解得x>  ,由f(x)在[2,+∞)上是增函数,
,由f(x)在[2,+∞)上是增函数,
可知  ≤2.解得0<a≤16
≤2.解得0<a≤16
综上可知实数a的取值范围是(-∞,16].

练习册系列答案
相关题目
 成立的充分不必要条件是
成立的充分不必要条件是 ,则实数
,则实数 的取值范围是______
的取值范围是______ 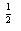 ,②y=log
,②y=log (x+1),③y=|x-1|,④y=2x+1,其中在区间(0,1)上单调递减的函数的序号是( )
(x+1),③y=|x-1|,④y=2x+1,其中在区间(0,1)上单调递减的函数的序号是( ) 内是单调递增的函数是( )
内是单调递增的函数是( ) B.
B. C.
C.  D.
D.
 C.
C. D.0
D.0 ,2)在幂函数y=f(x)的图象上,点
,2)在幂函数y=f(x)的图象上,点 在幂函数y=g(x)的图象上,若f(x)=g(x),则x=________.
在幂函数y=g(x)的图象上,若f(x)=g(x),则x=________. 的零点所在的区间为( )
的零点所在的区间为( )