题目内容
(本小题满分12分)已知:过抛物线 的焦点
的焦点 的直线交抛物线于
的直线交抛物线于 两个不同的点,过
两个不同的点,过 分别作抛物线的切线,且二者相交于点
分别作抛物线的切线,且二者相交于点

(1)求证: ;
;
(2)求 的面积的最小值。
的面积的最小值。
(1)详见解析;(2)4.
【解析】
试题分析:(1) 设LAB: ,代入
,代入 得
得 ,又设
,又设 ,利用韦达定理和导数的几何意义求出点C的坐标从而证明
,利用韦达定理和导数的几何意义求出点C的坐标从而证明 ;
;
(2) 由(1)知,点C到AB的距离 ,另由抛物线的焦点弦长公式求出
,另由抛物线的焦点弦长公式求出 ,从而将三角形ABC的面积表示成
,从而将三角形ABC的面积表示成 的函数转化为函数的最值问题.
的函数转化为函数的最值问题.
试题解析:(1)证明:设LAB: ,代入
,代入 得
得
 2分
2分
因为

 5分
5分


①若 ,则
,则 ,所以
,所以 .
.
所以 6分
6分
②若k=0,显然 7分
7分
(或

 7分)
7分)
(2)解由(1)知,点C到AB的距离 8分
8分



所以当 时,
时, 面积的最小值是4. 12分
面积的最小值是4. 12分
考点:1、抛物线的标准方程及几何性质;2、导数的几何意义;3、平面向量的数量积。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
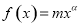 的图象经过点
的图象经过点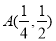 ,则它在点A处的切线方程是( )
,则它在点A处的切线方程是( )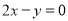 B.
B.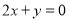
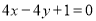 D.
D.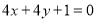

 B.
B. C.
C. D.
D.
 表示圆,则实数
表示圆,则实数 的取值范围是_______________
的取值范围是_______________ (C)
(C) (D)
(D)
 中,内角
中,内角 所对的边分别为
所对的边分别为 ,且
,且 。
。 ;
; ,求
,求 ,则它们的图象可能是( )
,则它们的图象可能是( )
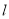 过椭圆
过椭圆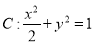 的左焦点
的左焦点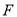 ,且与椭圆
,且与椭圆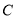 交于
交于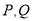 两点,
两点,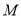 为弦
为弦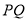 的中点,
的中点,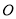 为原点,若
为原点,若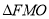 是以线段
是以线段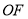 为底边的等腰三角形,则直线
为底边的等腰三角形,则直线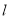 的斜率为
的斜率为