题目内容
15.若直线y=1与函数f(x)=2sin2x的图象相交于点P(x1,y1),Q(x2,y2),且|x1-x2|=$\frac{2π}{3}$,则线段PQ与函数f(x)的图象所围成的图形面积是( )| A. | $\frac{2π}{3}+\sqrt{3}$ | B. | $\frac{π}{3}+\sqrt{3}$ | C. | $\frac{2π}{3}+\sqrt{3}-2$ | D. | $\frac{π}{3}+\sqrt{3}-2$ |
分析 根据直线y=1与函数f(x)=2sin2x的图象相交于点P(x1,y1),Q(x2,y2),求解x1,x2的值,利用定积分即可求解线段PQ与函数f(x)的图象所围成的图形面积.
解答 解:函数f(x)=2sin2x,
周期T=π,
令2sin2x=1,解得:x=$kπ+\frac{π}{12}$或$kπ+\frac{5π}{6}$,
直线y=1与函数f(x)=2sin2x的图象相交于点从左向右依次是$\frac{π}{12}$,$\frac{5π}{12}$,$\frac{13π}{12}$…,
∵|x1-x2|=$\frac{2π}{3}$
令x1=$\frac{5π}{12}$,x2=$\frac{13π}{12}$,
可得:线段PQ与函数f(x)的图象所围成的图形面积
S=$\frac{2π}{3}×1$-2${∫}_{\frac{5π}{12}}^{\frac{π}{2}}2sin2xdx$-2${∫}_{\frac{π}{2}}^{\frac{3π}{4}}2sin2xdx$=$\frac{2π}{3}+\sqrt{3}$.
故选A
点评 本题考查了本题给出正弦型三角函数的图象与直线y=1的图象相交于点问题的运用以及定积分的求法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.$f(x)=Asin(ωx+φ)(A>0,ω>0,-\frac{π}{2}<φ<\frac{π}{2})$的部分图象如图所示,则函数f(x)的解析式为( )


| A. | $f(x)=2sin(2x-\frac{π}{6})$ | B. | $f(x)=2sin(x+\frac{π}{6})$ | C. | $f(x)=2sin(2x+\frac{π}{3})$ | D. | $f(x)=2sin(2x+\frac{π}{6})$ |
11.数列{an}满足a1=3,Sn=nan-n(n-1)
(Ⅰ) 求数列{an}的通项公式an;
(Ⅱ)令bn=$\frac{1}{{{a_n}•{a_{n+1}}}}$,求数列{bn}的前n项和Tn.
(Ⅰ) 求数列{an}的通项公式an;
(Ⅱ)令bn=$\frac{1}{{{a_n}•{a_{n+1}}}}$,求数列{bn}的前n项和Tn.
8.设f(x)为定义在R上的奇函数,且满足f(x)=f(x+4),f(1)=1,则f(-1)+f(8)=( )
| A. | -2 | B. | -1 | C. | 0 | D. | 1 |
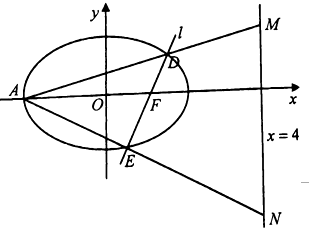 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为F,短轴长为2$\sqrt{3}$,点P为椭圆C上一点,且点P到点F的最远距离是最近距离的3倍.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为F,短轴长为2$\sqrt{3}$,点P为椭圆C上一点,且点P到点F的最远距离是最近距离的3倍.