题目内容
10.△ABC的内角A,B,C的对边分别为a,b,c,已知a=bcosC+csinB,则B=$\frac{π}{4}$.分析 利用正弦定理和三角形内角和定理消去A,和差公式打开可得B的大小.
解答 解:由a=bcosC+csinB以及正弦定理:
可得:sinA=sinBcosC+sinCsinB
?sinBcosC+sinCcosB=sinBcosC+sinCsinB
∴sinCcosB=sinCsinB
∵sinC≠0
∴cosB=sinB
0<B<π,
∴B=$\frac{π}{4}$.
故答案为$\frac{π}{4}$.
点评 本题考了正弦定理和三角形内角和定理以及两角和与差的计算.属于基础题.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
18.设$f(x)=\left\{\begin{array}{l}{2^x},x∈[{0,2}]\\ x+1,x∈[{-2,0})\end{array}\right.$,在集合M={y|y=f(x)}中随机取一个数m,则事件“m>0”的概率为( )
| A. | $\frac{3}{4}$ | B. | $\frac{1}{4}$ | C. | $\frac{4}{5}$ | D. | $\frac{1}{5}$ |
15.若直线y=1与函数f(x)=2sin2x的图象相交于点P(x1,y1),Q(x2,y2),且|x1-x2|=$\frac{2π}{3}$,则线段PQ与函数f(x)的图象所围成的图形面积是( )
| A. | $\frac{2π}{3}+\sqrt{3}$ | B. | $\frac{π}{3}+\sqrt{3}$ | C. | $\frac{2π}{3}+\sqrt{3}-2$ | D. | $\frac{π}{3}+\sqrt{3}-2$ |
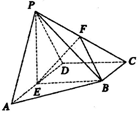 在四棱锥P-ABCD中,E为棱AD的中点,PE⊥平面ABCD,AD∥BC,∠ADC=90°,ED=BC=2,EB=3,F为棱PC的中点.
在四棱锥P-ABCD中,E为棱AD的中点,PE⊥平面ABCD,AD∥BC,∠ADC=90°,ED=BC=2,EB=3,F为棱PC的中点.