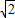Question

过原点O作两条相互垂直的直线分别与椭圆P：

x2

2

+y2=1交于A、C与B、D，则四边形ABCD面积最小值为

2

2

．

Answer 1

分析：先设出A、B 两点的坐标，则四边形ABCD面积等于 4×S_△AOB，化简为2

2+ 1 4 sin2 2α

，求出其最小值．

解答：解：由题意可得四边形ABCD的对角线互相垂直，且四个顶点在椭圆

x2

2

+y2=1上．
可设A（

2

cosα，sinα ），B（

2

cos（α+90°），sin（α+90°）），0°≤α≤180°．
则四边形ABCD面积等于4×S_△AOB=4×

1

2

|OA|•|OB|=2

2cos2α+sin2α

×

2cos2(α+90°)+sin2(α+90°)

=2

(1+cos2α)(1+sin2α)

=2

2+ 1 4 sin2 2α

≥2

2

当且仅当sin2α=0，即 α=0°或180°时，等号成立．
故四边形ABCD面积的最小值等于2

2

．
故答案为：2

2

点评：本题的考点是椭圆的简单性质，主要考查直线和圆锥曲线的位置关系，考查同角三角函数的基本关系，正确化简，利用三角函数的最值，是解题的关键．