题目内容
过原点O作两条相互垂直的直线分别与椭圆P: 交于A、C与B、D,则四边形ABCD面积最小值为( )
交于A、C与B、D,则四边形ABCD面积最小值为( )A.

B.4
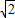
C.2

D.

【答案】分析:由题意可得四边形ABCD面积等于 ,当AC和BD中,有一条直线的斜率不存在时,求得四边形ABCD面积等于
,当AC和BD中,有一条直线的斜率不存在时,求得四边形ABCD面积等于
2 .当AC和BD的斜率都存在时,设AC的方程为y=kx,BD方程为y=-
.当AC和BD的斜率都存在时,设AC的方程为y=kx,BD方程为y=- x.y=kx代入椭圆的方程化简,利用根与系数的关系及弦长公式求得AC的值,同理求得BD的值,化简
x.y=kx代入椭圆的方程化简,利用根与系数的关系及弦长公式求得AC的值,同理求得BD的值,化简  为
为 ,再利用基本不等式
,再利用基本不等式
求得它的最小值,综合可得结论.
解答:解:由题意可得四边形ABCD的对角线互相垂直,且四个顶点在椭圆 上,且a=
上,且a= ,b=1.
,b=1.
四边形ABCD面积等于 .
.
当AC和BD中,有一条直线的斜率不存在时,AC和BD的长度分别为2a和 2b,
四边形ABCD面积等于 =2ab=2
=2ab=2 ×1=2
×1=2 .
.
当AC和BD的斜率都存在时,设AC的方程为y=kx,BD方程为y=- x.
x.
把y=kx代入椭圆的方程化简为(2k2+1)x2-2=0,∴xA+xC=0, .
.
∴AC= •|xA-xC|=
•|xA-xC|= •
• =2
=2  .
.
同理求得 BD=2 ,
,
∴ =4
=4  =
= =
= =
=
= ≥
≥ =4×
=4× =
= ,当且仅当
,当且仅当 时,取等号.
时,取等号.
综上可得,四边形ABCD面积的最小值等于 .
.
故选:A.
点评:本题考查直线和圆锥曲线的位置关系,两条直线垂直的性质,基本不等式的应用,体现了分类讨论的数学思想,
属于中档题.
 ,当AC和BD中,有一条直线的斜率不存在时,求得四边形ABCD面积等于
,当AC和BD中,有一条直线的斜率不存在时,求得四边形ABCD面积等于2
 .当AC和BD的斜率都存在时,设AC的方程为y=kx,BD方程为y=-
.当AC和BD的斜率都存在时,设AC的方程为y=kx,BD方程为y=- x.y=kx代入椭圆的方程化简,利用根与系数的关系及弦长公式求得AC的值,同理求得BD的值,化简
x.y=kx代入椭圆的方程化简,利用根与系数的关系及弦长公式求得AC的值,同理求得BD的值,化简  为
为 ,再利用基本不等式
,再利用基本不等式求得它的最小值,综合可得结论.
解答:解:由题意可得四边形ABCD的对角线互相垂直,且四个顶点在椭圆
 上,且a=
上,且a= ,b=1.
,b=1.四边形ABCD面积等于
 .
.当AC和BD中,有一条直线的斜率不存在时,AC和BD的长度分别为2a和 2b,
四边形ABCD面积等于
 =2ab=2
=2ab=2 ×1=2
×1=2 .
.当AC和BD的斜率都存在时,设AC的方程为y=kx,BD方程为y=-
 x.
x.把y=kx代入椭圆的方程化简为(2k2+1)x2-2=0,∴xA+xC=0,
 .
.∴AC=
 •|xA-xC|=
•|xA-xC|= •
• =2
=2  .
.同理求得 BD=2
 ,
,∴
 =4
=4  =
= =
= =
=
=
 ≥
≥ =4×
=4× =
= ,当且仅当
,当且仅当 时,取等号.
时,取等号.综上可得,四边形ABCD面积的最小值等于
 .
.故选:A.
点评:本题考查直线和圆锥曲线的位置关系,两条直线垂直的性质,基本不等式的应用,体现了分类讨论的数学思想,
属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
过原点O作两条相互垂直的直线分别与椭圆P:
+y2=1交于A、C与B、D,则四边形ABCD面积最小值为( )
| x2 |
| 2 |
A、
| ||
B、4
| ||
C、2
| ||
D、
|