题目内容
已知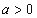 ,函数
,函数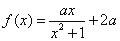 ,
,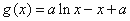 .
.
(Ⅰ)求函数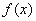 的单调区间;
的单调区间;
(Ⅱ)求证:对于任意的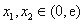 ,都有
,都有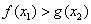 .
.
解:(Ⅰ)函数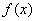 的定义域为
的定义域为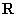 ,
,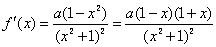 ,
,
因为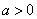 ,
,
所以,当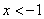 ,或
,或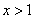 时,
时,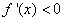 ;
;
当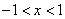 时,
时,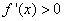 .
.
所以,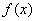 的单调递增区间为
的单调递增区间为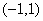 ,单调递减区间为
,单调递减区间为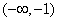 ,
,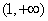 .
.
……6分
(Ⅱ)因为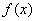 在区间
在区间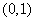 上单调递增,在区间
上单调递增,在区间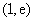 上单调递减,
上单调递减,
又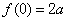 ,
,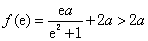 ,
,
所以,当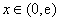 时,
时, .
.
由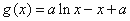 ,可得
,可得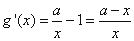 .
.
所以当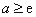 时,函数
时,函数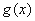 在区间
在区间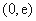 上是增函数,
上是增函数,
所以,当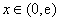 时,
时,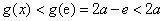 .
.
所以,当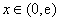 时,
时,
对于任意的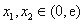 ,都有
,都有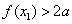 ,
,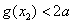 ,所以
,所以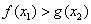 .
.
当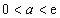 时,函数
时,函数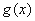 在区间
在区间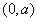 上是增函数,在区间
上是增函数,在区间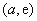 上是减函数,
上是减函数,
所以,当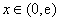 时,
时,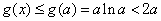 .
.
所以,当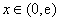 时,
时,
对于任意的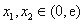 ,都有
,都有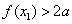 ,
,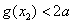 ,所以
,所以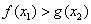 .
.
综上,对于任意的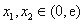 ,都有
,都有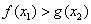 . ……………13分
. ……………13分

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
 =1渐近线上的一个动点P总在平面区域(x-m)2+y2≥16内,则实数m的取值范围是________.
=1渐近线上的一个动点P总在平面区域(x-m)2+y2≥16内,则实数m的取值范围是________. (B)
(B)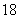
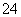 (D)
(D)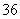
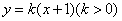 与抛物线
与抛物线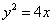 相交于
相交于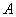 ,
,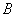 两点,且
两点,且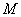 ,
, ,若
,若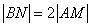 ,则
,则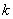 的值是 .
的值是 .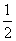 B.
B.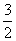
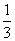
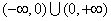 上的函数
上的函数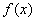 ,如果对于任意给定的等比数列
,如果对于任意给定的等比数列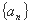 ,有
,有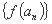 仍是等比数列,则称
仍是等比数列,则称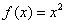 ; ②
; ②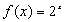 ; ③
; ③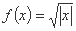 ; ④
; ④ ,则其中是“保等比数列函数”的
,则其中是“保等比数列函数”的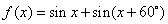 的最大值是
的最大值是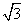 B.
B.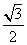 C.2 D.1
C.2 D.1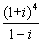 ,则
,则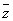 = ( )
= ( )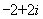 B.
B.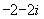 C.
C. D.
D.