题目内容
已知二次函数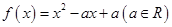 同时满足:
同时满足:
①不等式 的解集有且只有一个元素;
的解集有且只有一个元素;
②在定义域内存在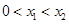 ,使得不等式
,使得不等式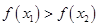 成立.
成立.
数列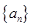 的通项公式为
的通项公式为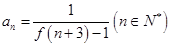 .
.
(1)求函数 的表达式;
的表达式;
(2)求数列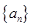 的前
的前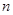 项和
项和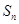 .
.
(1) ;(2)
;(2) .
.
解析试题分析:(1)首先根据二次函数 的开口方向以及不等式
的开口方向以及不等式 的解集只有一个元素这些条件得到
的解集只有一个元素这些条件得到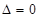 ,结合函数
,结合函数 在区间
在区间 上的单调性得出
上的单调性得出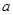 的值,进而求出函数
的值,进而求出函数 的解析式;(2)先求出数列
的解析式;(2)先求出数列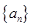 的通项公式
的通项公式 ,利用裂项相消法求数列
,利用裂项相消法求数列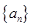 的前
的前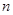 项和
项和 .
.
试题解析:(1) ,且不等式
,且不等式 的解集有且只有一个元素,
的解集有且只有一个元素,
则 ,解得
,解得 或
或 ,
,
又由于定义域内存在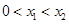 ,有
,有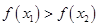 ,则函数
,则函数 在区间
在区间 上不是增函数,
上不是增函数,
因此 ,所以
,所以 ,
, ;
;
(2) ,
,
所以
 .
.
考点:1.二次函数的解析式;2.裂项相消法求和

练习册系列答案
相关题目
 的前n项和为
的前n项和为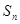 ,公差
,公差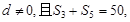
 成等比数列
成等比数列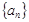 的通项公式;
的通项公式;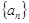 中依次取出第2项、第4项、第8项,
中依次取出第2项、第4项、第8项,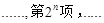 ,按原来顺序组成一个新数列
,按原来顺序组成一个新数列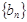 ,且这个数列的前
,且这个数列的前 的表达式.
的表达式.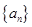 的前
的前 项和为
项和为 ,且
,且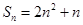 ,
, ,数列
,数列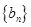 满足
满足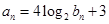 ,
,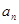 ,
,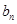 ;
;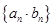 的前
的前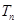 .
.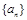 的前n项和为
的前n项和为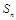 ,且
,且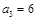 ,
,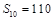 .
.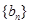 前n项和为
前n项和为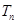 ,且
,且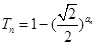 ,令
,令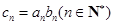 .求数列
.求数列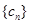 的前n项和
的前n项和 .
.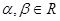 且
且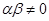 ,数列
,数列 满足
满足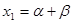 ,
,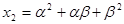 ,
,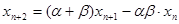 (
(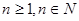 ),令
),令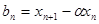 ,
,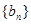 是等比数列;
是等比数列;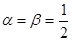 ,求
,求 项和
项和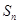 .
.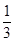 )是函数
)是函数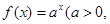 且
且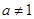 )的图象上一点,等比数列
)的图象上一点,等比数列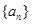 的前
的前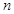 项和为
项和为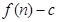 ,数列
,数列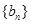
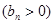 的首项为
的首项为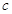 ,且前
,且前 满足
满足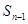 =
=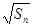 +
+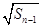 (
( ).
).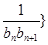 前
前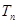 .
.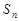 为数列
为数列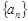 的前
的前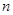 项和,且
项和,且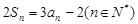 .
.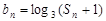 ,求数列
,求数列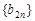 的前n项和
的前n项和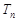 .
.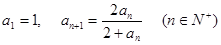 ,试猜想这个数列的通项公式。
,试猜想这个数列的通项公式。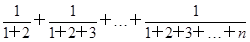 .
.