题目内容
已知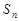 为数列
为数列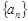 的前
的前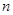 项和,且
项和,且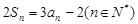 .
.
(Ⅰ)求数列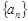 的通项公式;
的通项公式;
(Ⅱ)若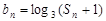 ,求数列
,求数列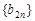 的前n项和
的前n项和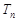 .
.
(Ⅰ)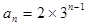 ;(Ⅱ)
;(Ⅱ) 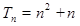 .
.
解析试题分析:(Ⅰ)由数列的递推公式求数列通项公式;(Ⅱ)根据(Ⅰ)通项公式得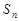 ,再得
,再得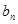 ,从而得
,从而得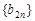 的通项公式,进而求得
的通项公式,进而求得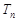 .
.
试题解析:解:(Ⅰ)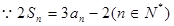 ,
,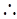 当
当 时,
时, ,
,
两式相减得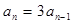 , 3分
, 3分
又当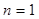 时,
时, , 4分
, 4分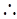 数列
数列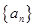 是首项为2,公比为3的等比数列, 6分
是首项为2,公比为3的等比数列, 6分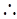 数列
数列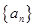 的通项公式是
的通项公式是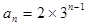 .
.
(Ⅱ)由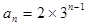 可得
可得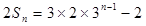 ,
, , 8分
, 8分 , 10分
, 10分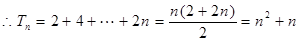 . 12分
. 12分
考点:1、数列的递推公式;2、通项公式;3、前n项和公式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 )
) .
. 同时满足:
同时满足: 的解集有且只有一个元素;
的解集有且只有一个元素;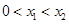 ,使得不等式
,使得不等式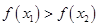 成立.
成立.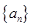 的通项公式为
的通项公式为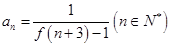 .
. 的表达式;
的表达式; 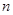 项和
项和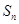 .
.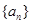 的前
的前 项和
项和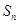 ,满足:
,满足: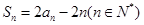 .
.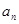 ;
;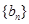 的满足
的满足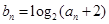 ,
,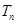 为数列
为数列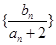 的前
的前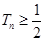 .
.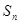 为数列{
为数列{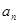 }的前项和,已知
}的前项和,已知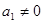 ,2
,2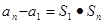 ,
, N
N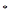
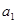 ,
,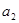 ,并求数列{
,并求数列{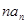 }的前
}的前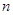 项和。
项和。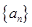 的前n项和为
的前n项和为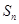 ,点
,点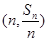 在直线
在直线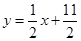 上.数列{bn}满足
上.数列{bn}满足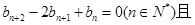
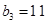 ,前9项和为153.
,前9项和为153.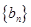 的通项公式;
的通项公式;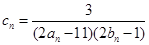 ,数列
,数列 的前n和为
的前n和为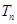 ,求使不等式
,求使不等式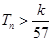 对一切
对一切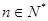 都成立的最大正整数k的值.
都成立的最大正整数k的值. 的前n项和为
的前n项和为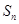 ,已知
,已知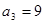 ,
, 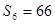 .
.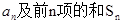 ;
;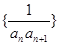 的前n项和为
的前n项和为 ,证明:
,证明: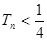 ;
;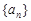 满足:
满足: ,数列
,数列 满足
满足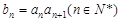 .
.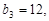 求
求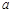 的值及
的值及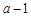 的等比数列,问是否存在正实数
的等比数列,问是否存在正实数 ,使得数列
,使得数列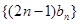 的前
的前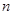 项和
项和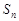 (用n,
(用n,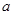 表示).
表示). 满足:
满足: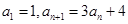 ;
;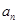 ;
;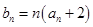 ,求数列
,求数列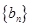 的前
的前 项和为
项和为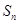 。
。