题目内容
已知x,y>0,求证:| x+y |
| 2 |
| xy |
分析:要证
≥
,只要证(
)2≥xy,即证(x+y)2≥4xy,即证(x-y)2≥0,并在当且仅当x=y时取等号.
| x+y |
| 2 |
| xy |
| x+y |
| 2 |
解答:证明:要证
≥
,
只要证(
)2≥xy,
即证(x+y)2≥4xy,
即证(x-y)2≥0,
而上式显然成立,
并在当且仅当x=y时取等号,
所以原不等式成立.
| x+y |
| 2 |
| xy |
只要证(
| x+y |
| 2 |
即证(x+y)2≥4xy,
即证(x-y)2≥0,
而上式显然成立,
并在当且仅当x=y时取等号,
所以原不等式成立.
点评:本题考查不等式的证明,解题时要注意分析法在证明中的合理运用.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
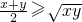 ,并说明等号成立的条件.
,并说明等号成立的条件. ,并说明等号成立的条件.
,并说明等号成立的条件.