题目内容
12.(文科)已知m∈R,集合A={m|m2-am<12a2(a≠0)};集合B={m|方程$\frac{{x}^{2}}{m+4}$+$\frac{{y}^{2}}{8-m}$=1表示焦点在y轴上的椭圆},若“m∈A”是“m∈B”的充分不必要条件,求a的取值范围.分析 通过讨论a的范围,分别求出关于A、B的不等式的解集,结合集合的包含关系,得到关于a的不等式组,解出即可.
解答 解:对于集合A,由m2-am<12a2,故(m-4a)(m+3a)<0,
对于集合B,解$\left\{\begin{array}{l}{m+4>0}\\{8-m>0}\\{m+4<8-m}\end{array}\right.$,解得:-4<m<2;
①a>0时,集合A:-3a<m<4a,
若“m∈A”是“m∈B”的充分不必要条件,
则$\left\{\begin{array}{l}{-4<-3a}\\{4a<2}\end{array}\right.$,解得:0<a<$\frac{1}{2}$;
②a<0时,集合A:a<m<-3a,
若“m∈A”是“m∈B”的充分不必要条件,
则$\left\{\begin{array}{l}{-4<4a}\\{-3a<2}\end{array}\right.$,解得:-$\frac{2}{3}$<a<0,
综上:a∈(-$\frac{2}{3}$,0)∪(0,$\frac{1}{2}$).
点评 本题考查了充分必要条件,考查集合的运算以及不等式问题,是一道中档题.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
17.执行如图所示的程序框图,则输出S的值是( )
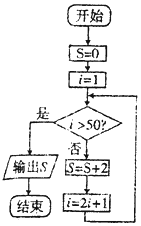

| A. | 10 | B. | 12 | C. | 100 | D. | 102 |
4.数列{an}中,a3=1,a5=1,如果数列{$\frac{1}{{a}_{n}+1}$}是等差数列,则a11=( )
| A. | 1 | B. | $\frac{1}{11}$ | C. | -$\frac{1}{13}$ | D. | -$\frac{1}{7}$ |