题目内容
17.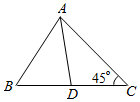 如图,在△ABC中,点D在边BC上,BD=2,BA=3,AD=$\sqrt{7}$,∠C=45°.
如图,在△ABC中,点D在边BC上,BD=2,BA=3,AD=$\sqrt{7}$,∠C=45°.(1)求∠B的大小;
(2)求△ABD的面积及边AC的长.
分析 (1)直接利用余弦定理化简求解即可.
(2)利用三角形的面积以及正弦定理求解即可.
解答 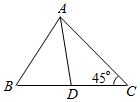 解:(1)在△ABD中,由余弦定理,得
解:(1)在△ABD中,由余弦定理,得
$cos∠B=\frac{{B{A^2}+B{D^2}-A{D^2}}}{2BA•BD}$=$\frac{{{3^2}+{2^2}-{{(\sqrt{7})}^2}}}{2×3×2}=\frac{1}{2}$.…(5分)
又0°<∠B<180°,所以∠B=60°.…(6分)
(2)${S_{△ABD}}=\frac{1}{2}BA•BD•sin∠B=\frac{1}{2}×3×2×\frac{{\sqrt{3}}}{2}=\frac{{3\sqrt{3}}}{2}$.…(9分)
在△ABC中,由正弦定理,得$\frac{AC}{sin∠B}=\frac{AB}{sin∠C}$,
即$\frac{AC}{sin60°}=\frac{3}{sin45°}$.解得$AC=\frac{{3\sqrt{6}}}{2}$.…(12分)
点评 本题考查正弦定理与余弦定理的应用,考查转化思想以及计算能力.

练习册系列答案
相关题目
8.若tanα=$\frac{1}{3}$,则cos($\frac{π}{2}$+2α)=( )
| A. | -$\frac{4}{5}$ | B. | -$\frac{3}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
5.设变量x,y满足约束条件$\left\{\begin{array}{l}{2x-y+2≥0}\\{4x-y-2≤0}\\{x≥0,y≥0}\end{array}\right.$,目标函数z=abx+y(a,b均大于0)的最大值为8,则a+b的最小值为( )
| A. | 8 | B. | 4 | C. | 2$\sqrt{2}$ | D. | 2 |
12.已知数列{bn}满足b1=$\frac{1}{2}$,2bn+1-bn•bn+1=1,则b1+$\frac{{b}_{2}}{{2}^{2}}$+$\frac{{b}_{3}}{{3}^{2}}$+…+$\frac{{b}_{100}}{10{0}^{2}}$=( )
| A. | $\frac{97}{100}$ | B. | $\frac{99}{100}$ | C. | $\frac{100}{101}$ | D. | $\frac{102}{101}$ |
9.若a>b,c>d,则下面不等式中成立的一个是( )
| A. | a+d>b+c | B. | ac>bd | C. | ac2>bc2 | D. | d-a<c-b |
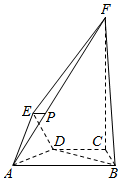 如图几何体中,四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°,CB=CD=2.面EAD⊥面ABCD,面FCB⊥面ABCD,且CF⊥BC.
如图几何体中,四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°,CB=CD=2.面EAD⊥面ABCD,面FCB⊥面ABCD,且CF⊥BC.