题目内容
【题目】数学中有许多形状优美、寓意美好的曲线,例如:四叶草曲线就是其中一种,其方程为![]() .给出下列四个结论:
.给出下列四个结论:
①曲线![]() 有四条对称轴;
有四条对称轴;
②曲线![]() 上的点到原点的最大距离为
上的点到原点的最大距离为![]() ;
;
③曲线![]() 第一象限上任意一点作两坐标轴的垂线与两坐标轴围成的矩形面积最大值为
第一象限上任意一点作两坐标轴的垂线与两坐标轴围成的矩形面积最大值为![]() ;
;
④四叶草面积小于![]() .
.
其中,所有正确结论的序号是( )

A.①②B.①③C.①③④D.①②④
【答案】C
【解析】
①利用![]() 之间的代换判断出对称轴的条数;②利用基本不等式求解出到原点的距离最大值;③将面积转化为
之间的代换判断出对称轴的条数;②利用基本不等式求解出到原点的距离最大值;③将面积转化为![]() 的关系式,然后根据基本不等式求解出最大值;④根据
的关系式,然后根据基本不等式求解出最大值;④根据![]() 满足的不等式判断出四叶草与对应圆的关系,从而判断出面积是否小于
满足的不等式判断出四叶草与对应圆的关系,从而判断出面积是否小于![]() .
.
①:当![]() 变为
变为![]() 时,
时, ![]() 不变,所以四叶草图象关于
不变,所以四叶草图象关于![]() 轴对称;
轴对称;
当![]() 变为
变为![]() 时,
时,![]() 不变,所以四叶草图象关于
不变,所以四叶草图象关于![]() 轴对称;
轴对称;
当![]() 变为
变为![]() 时,
时,![]() 不变,所以四叶草图象关于
不变,所以四叶草图象关于![]() 轴对称;
轴对称;
当![]() 变为
变为![]() 时,
时,![]() 不变,所以四叶草图象关于
不变,所以四叶草图象关于![]() 轴对称;
轴对称;
综上可知:有四条对称轴,故正确;
②:因为![]() ,所以
,所以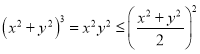 ,
,
所以![]() ,所以
,所以![]() ,取等号时
,取等号时![]() ,
,
所以最大距离为![]() ,故错误;
,故错误;
③:设任意一点![]() ,所以围成的矩形面积为
,所以围成的矩形面积为![]() ,
,
因为![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
取等号时![]() ,所以围成矩形面积的最大值为
,所以围成矩形面积的最大值为![]() ,故正确;
,故正确;
④:由②可知![]() ,所以四叶草包含在圆
,所以四叶草包含在圆![]() 的内部,
的内部,
因为圆的面积为:![]() ,所以四叶草的面积小于
,所以四叶草的面积小于![]() ,故正确.
,故正确.
故选:C.

练习册系列答案
相关题目