Question

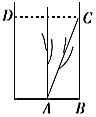
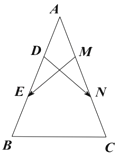
【题目】如图，在等腰△ABC中，AB＝AC＝3，D，E与M，N分别是AB，AC的三等分点，且1，则tanA＝_____，_____．

Answer 1

【答案】 ．

【解析】

设A（0，b），B（﹣a，0），C（a，0），利用1以及可求得a，b，在△ABC中利用余弦定理求得，从而可得；利用数量积的定义计算.

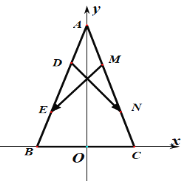
以边BC所在直线为x轴，以边BC的中垂线为y轴，建立如图所示平面直角坐标系，

设A（0，b），B（﹣a，0），C（a，0），且D，E与M，N分别是AB，AC的三等分点，

∴D（，），E（，），M（ ，），N（ ，），

∴（a，），（﹣a，），且 1，

∴﹣a21①，

又AC＝3，∴a2+b2＝9②，

联立①②得，a2，

在△ABC中，由余弦定理得，cosA．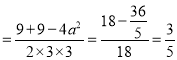

因为A为等腰三角形的顶角；且cosA，

∴sinA；

∴tanA；

sin；

∴cosB＝cos（）＝sin；

∴3×2a×cosB＝﹣3．

故答案为：（1）；（2）．