题目内容
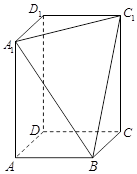
如图,直三棱柱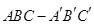 ,
,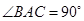 ,
,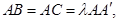 点M,N分别为
点M,N分别为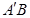 和
和 的中点.
的中点.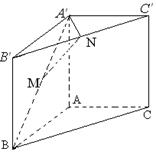
(Ⅰ)证明: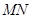 ∥平面
∥平面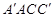 ;
;
(Ⅱ)若二面角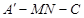 A为直二面角,求
A为直二面角,求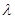 的值.
的值.
(Ⅰ)分别取 的中点
的中点 ,再连结
,再连结 ,得到
,得到 ,
,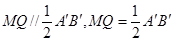 ,证得四边形
,证得四边形 为平行四边形,推出
为平行四边形,推出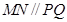 ,证得
,证得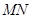 ∥平面
∥平面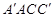 ;
;
(Ⅱ)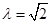 。
。
解析试题分析:(Ⅰ)分别取 的中点
的中点 ,再连结
,再连结 ,则有
,则有 ,
,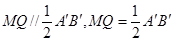 ,所以
,所以
则四边形 为平行四边形,所以
为平行四边形,所以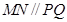 ,则
,则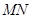 ∥平面
∥平面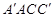 4分
4分
(Ⅱ)分别以 所在直线为
所在直线为 轴,建立空间直角坐标系(如图)
轴,建立空间直角坐标系(如图)
设 ,则
,则 ,所以平面
,所以平面 的一个法向量
的一个法向量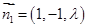 ,平面
,平面 的一个法向量
的一个法向量 ,
,
因为二面角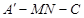 A为直二面角,所以
A为直二面角,所以 ,则有
,则有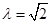 12分
12分
考点:本题主要考查立体几何中的平行关系、角的计算,空间向量的应用。
点评:典型题,立体几何题,是高考必考内容,往往涉及垂直关系、平行关系、角、距离、体积的计算。在计算问题中,有“几何法”和“向量法”。利用几何法,要遵循“一作、二证、三计算”的步骤,利用空间向量,省去繁琐的证明,也是解决立体几何问题的一个基本思路。注意运用转化与化归思想,将空间问题转化成平面问题。

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目



 的方向相同时,画出四棱锥
的方向相同时,画出四棱锥 的正视图(要求标出尺寸,并写出演算过程);
的正视图(要求标出尺寸,并写出演算过程);
 的体积.
的体积. 中,
中,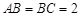 ,过
,过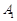 、
、 、
、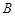 三点的平面截去长方体的一个角后,得到如图所示的几何体
三点的平面截去长方体的一个角后,得到如图所示的几何体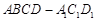 ,且这个几何体的体积为
,且这个几何体的体积为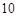 .
.
 的长;
的长; 到平面
到平面 的距离.
的距离.
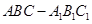 中,四边形
中,四边形 是正方形,
是正方形,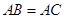 ,
, ,
,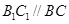 且
且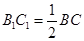 ,二面角
,二面角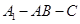 是直二面角
是直二面角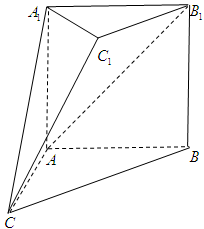
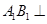 平面
平面 ;
; 平面
平面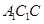 。
。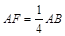 .
.
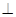 平面EFDC.
平面EFDC.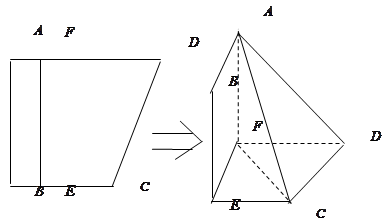
 ,是否在折叠后的AD上存在一点
,是否在折叠后的AD上存在一点 ,且
,且 ,使得CP∥平面ABEF?若存在,求出
,使得CP∥平面ABEF?若存在,求出 的值;若不存在,说明理由;
的值;若不存在,说明理由;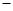 CDF的体积有最大值?并求出这个最大值.
CDF的体积有最大值?并求出这个最大值. EA=EC=6,M为EC中点,平面BCE⊥平面ACE,AE⊥EB
EA=EC=6,M为EC中点,平面BCE⊥平面ACE,AE⊥EB
 中,面
中,面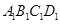 中心为
中心为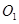 .
.
 面
面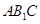 ;
;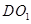 与
与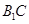 所成角.
所成角.