Question

方程x²+x+n=0（n∈（0，1））有实根的概率为（　　）

A．

B．

C．

D．

Answer 1

考点：

几何概型．

专题：

常规题型；计算题．

分析：

欲求图象恒在x轴上方的概率，则可建立关于a，b的直角坐标系，画出关于a和b的平面区域，再根据几何概型概率公式结合定积分求面积的方法易求解．

解答：

解：由于方程x²+x+n=0（n∈（0，1））有实根，

∴△≥0，

即1﹣4n≥0，⇒n≤，

又n∈（0，1），

∴有实根的概率为：P=，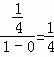

故选C．

点评：

本小题主要考查几何概型、几何概型的应用、二次方程等基础知识，考查计算能力．属于基础题．