题目内容
【题目】如图，三棱锥
中，底面
是边长为2的正三角形， 
， 
.
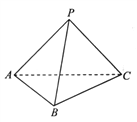
（1）求证：平面
平面
；
（2）若
，求三棱锥
的体积.
【答案】（1）见解析;（2）
.
【解析】【试题分析】（1）取
的中点
，连接
，利用等边三角形的性质，得到
，通过计算证明
，由此证明
平面
，从而得到平面
平面
.（2）利用（1）的结论，以
为高，计算体积
【试题解析】
（1）取AC的中点O，连接BO，PO.
因为ABC是边长为2的正三角形，
所以BO⊥AC，BO=
.
因为PA⊥PC，所以PO=
.
因为PB=2，所以OP2+OB2=PB2，所以PO⊥OB.
因为AC，OP为相交直线，所以BO⊥平面PAC.
又OB平面ABC，
所以平面PAB⊥平面ABC．
（2）因为PA=PC，PA⊥PC，AC=2，
所以
.
由（1）知BO⊥平面PAC.
所以
.
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
