题目内容
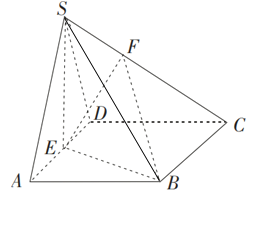
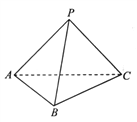
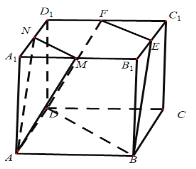
【题目】如图,正方体![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() ,
,![]() ,
,![]() 的中点.
的中点.

(Ⅰ)求证:![]() ,
,![]() ,
,![]() ,
,![]() 四点共面;
四点共面;
(Ⅱ)求证:平面![]() ∥平面
∥平面![]() ;
;
(Ⅲ)画出平面![]() 与正方体侧面的交线(需要有必要的作图说明、保留作图痕迹).
与正方体侧面的交线(需要有必要的作图说明、保留作图痕迹).
【答案】(Ⅰ)见解析;(Ⅱ)见解析;(Ⅲ)见解析
【解析】
(Ⅰ)要证![]() ,
,![]() ,
,![]() ,
,![]() 四点共面,只需证明
四点共面,只需证明![]() ∥
∥![]() ;
;
(Ⅱ)只需证明![]() ∥平面
∥平面![]() ,
,![]() ∥平面
∥平面![]() 即可;
即可;
(Ⅲ)因为![]() ∥平面
∥平面![]() ,
,![]() 平面
平面![]() ,设平面
,设平面![]() 平面
平面![]() ,由线面平行的性质定理知
,由线面平行的性质定理知![]() ∥
∥![]() ,过
,过![]() 作
作![]() 的平行线即可.
的平行线即可.
(Ⅰ)因为![]() 分别是
分别是![]() ,
,![]() 的中点,所以
的中点,所以![]() 为
为![]() 的中位线,所以
的中位线,所以![]() ∥
∥![]() ,
,
又四边形![]() 是矩形,所以
是矩形,所以![]() ∥
∥![]() ,所以
,所以![]() ∥
∥![]() ,故
,故![]() ,
,![]() ,
,![]() ,
,![]() 四点共面;
四点共面;
(Ⅱ)由已知,![]() 为
为![]() 的中位线,所以
的中位线,所以![]() ∥
∥![]() ,所以
,所以![]() ∥
∥![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() ∥平面
∥平面![]() ,
,
同理![]() ∥
∥![]() ∥
∥![]() ,且
,且![]()
![]()
![]() ,所以四边形
,所以四边形![]() 为平行四边形,
为平行四边形,
所以![]() ∥
∥![]() ,又
,又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() ∥平面
∥平面![]() ,
,
又![]() ,所以平面
,所以平面![]() ∥平面
∥平面![]() .
.
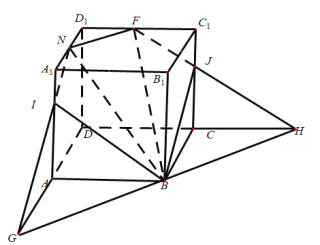
(Ⅲ)∴过![]() 作
作![]() 的平行线交
的平行线交![]() 分别于
分别于![]() ,连接
,连接![]() 分别交
分别交![]() 于
于![]() ,连接
,连接![]() ,如图,
,如图,
理由如下:因为![]() ∥
∥![]() ∥
∥![]() ,∴
,∴![]() ∥平面
∥平面![]() ,
,![]() 平面
平面![]() ,设平面
,设平面![]() 平面
平面![]() ,
,
由线面平行的性质定理知![]() ∥
∥![]() ,所以过
,所以过![]() 作
作![]() 的平行线交
的平行线交![]() 分别于
分别于![]() ,连
,连
接![]() 分别交
分别交![]() 于
于![]() ,连接
,连接![]() ,即可得到平面
,即可得到平面![]() 与正方体侧面的交
与正方体侧面的交
线.

【题目】某小组共有![]() 五位同学,他们的身高(单位:米)以及体重指标(单位:千克/米2)
五位同学,他们的身高(单位:米)以及体重指标(单位:千克/米2)
如下表所示:
A | B | C | D | E | |
身高 | 1.69 | 1.73 | 1.75 | 1.79 | 1.82 |
体重指标 | 19.2 | 25.1 | 18.5 | 23.3 | 20.9 |
(Ⅰ)从该小组身高低于![]() 的同学中任选
的同学中任选![]() 人,求选到的
人,求选到的![]() 人身高都在
人身高都在![]() 以下的概率
以下的概率
(Ⅱ)从该小组同学中任选![]() 人,求选到的
人,求选到的![]() 人的身高都在
人的身高都在![]() 以上且体重指标都在
以上且体重指标都在![]() 中的概率.
中的概率.
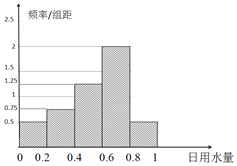
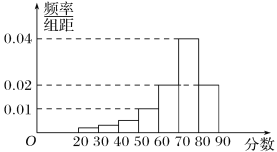
【题目】为达到节水节电的目的,某家庭记录了20天的日用电量xi(单位:度)的频数分布表和这20天相应的日用水量yi(单位:m3)的频率分布直方图如下:
日用电量xi | [0,2) | [2,4) | [4,6) | [6,8) | [8,10) |
频数(天) | 2 | 5 | 7 | 3 | 3 |
(1)假设水费为2.5元/m3,电费为0.6元/度,用以上数据估计该家庭日用电量的平均值和日用水量的平均值,并据此估计该家庭一个月的水费和电费一共是多少?(一个月按30天算,同一组中的数据以这组数据所在区间中点的值作代表);
(2)假设该家庭的日用水量y和日用电量x可用线性回归模型来拟合,请利用(1)中的计算数据及所给的参考数据和公式,建立y与x的回归方程,预测若该家庭日用电量为20度时的日用水量是多少m3?(回归方程的系数小数点后保留2位小数)
参考数据:![]() xiyi=65,
xiyi=65,![]() 612
612
参考公式:回归方程![]() x
x![]() 中斜率和截距的公式分别为:
中斜率和截距的公式分别为:
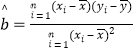 ,
,![]()