题目内容
15.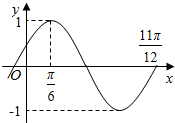 设函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,为了得到函数y=cos2x的图象,只需将函数y=f(x)的图象( )
设函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,为了得到函数y=cos2x的图象,只需将函数y=f(x)的图象( )| A. | 向左平移$\frac{π}{6}$个单位 | B. | 向右平移$\frac{π}{6}$个单位 | ||
| C. | 向左平移$\frac{π}{3}$个单位 | D. | 向右平移$\frac{π}{3}$个单位 |
分析 由条件利用诱导公式、y=Asin(ωx+φ)的图象变换规律,得出结论.
解答 解:根据函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象,可得A=1,
$\frac{3}{4}$T=$\frac{3}{4}•\frac{2π}{ω}$=$\frac{11π}{12}$-$\frac{π}{6}$,求得ω=2,再根据五点法作图可得2×$\frac{π}{6}$+φ=$\frac{π}{2}$,
求得φ=$\frac{π}{6}$,故f(x)=sin(2x+$\frac{π}{6}$).
故将函数y=f(x)的图象向左平移$\frac{π}{6}$个单位,可得y=sin[2(x+$\frac{π}{6}$)+$\frac{π}{6}$]=sin(2x+$\frac{π}{2}$)=cos2x的图象,
故选:A.
点评 本题主要考查利用了y=Asin(ωx+φ)的图象变换规律,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.已知A(4,1,3),B(2,-5,1),C(3,7,-5),则平行四边形ABCD的顶点D的坐标是( )
| A. | (2,4,-1) | B. | (2,3,1) | C. | (-3,1,5) | D. | (5,13,-3) |
10.已知F1,F2分别是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左右焦点,若在双曲线的右支上存在一点M,使得($\overrightarrow{OM}$+$\overrightarrow{O{F}_{2}}$)•$\overrightarrow{{F}_{2}M}$=0 (其中O为坐标原点),且|$\overrightarrow{M{F}_{1}}$|=$\sqrt{3}$|$\overrightarrow{M{F}_{2}}$|,则双曲线的离心率为( )
| A. | $\sqrt{5}$-1 | B. | $\frac{\sqrt{3}+1}{2}$ | C. | $\frac{\sqrt{5}+1}{2}$ | D. | $\sqrt{3}$+1 |
3.设函数f(x)=$\left\{\begin{array}{l}{3x-b,x<1}\\{{2}^{x},x≥1}\end{array}\right.$,若f[f($\frac{1}{3}$)]=4,则b=( )
| A. | 1 | B. | -$\frac{1}{4}$ | C. | -$\frac{1}{4}$或1 | D. | -1 |
4.f(x)是定义在R上的奇函数,f(-3)=2,则下列各点在函数f(x)图象上的是( )
| A. | (3,-2) | B. | (3,2) | C. | (-3,-2) | D. | (2,-3) |
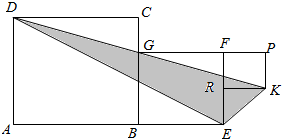 正方形ABCD、正方形BEFG和正方形RKPF的位置如图所示,点G在线段DK上,正方形BEFG的边长为4,则△DEK的面积为( )
正方形ABCD、正方形BEFG和正方形RKPF的位置如图所示,点G在线段DK上,正方形BEFG的边长为4,则△DEK的面积为( )