题目内容
10．已知F1，F2分别是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左右焦点，若在双曲线的右支上存在一点M，使得（$\overrightarrow{OM}$+$\overrightarrow{O{F}_{2}}$）•$\overrightarrow{{F}_{2}M}$=0 （其中O为坐标原点），且|$\overrightarrow{M{F}_{1}}$|=$\sqrt{3}$|$\overrightarrow{M{F}_{2}}$|，则双曲线的离心率为（ ）| A． | $\sqrt{5}$-1 | B． | $\frac{\sqrt{3}+1}{2}$ | C． | $\frac{\sqrt{5}+1}{2}$ | D． | $\sqrt{3}$+1 |
分析 依题意双曲线右支上存在一点M，使得（$\overrightarrow{OM}$+$\overrightarrow{O{F}_{2}}$）•$\overrightarrow{{F}_{2}M}$=0判断出∠F1MF2=90°，设出|MF2|=t，则|MF1|=$\sqrt{3}$t，进而利用双曲线定义可用t表示出a，根据勾股定理求得t和c的关系，最后可求得双曲线的离心率．
解答 解：∵双曲线右支上存在一点M，使得（$\overrightarrow{OM}$+$\overrightarrow{O{F}_{2}}$）•$\overrightarrow{{F}_{2}M}$=0，
∴∠F1MF2=90°
设|MF2|=t，则|MF1|=$\sqrt{3}$t，
∴a=$\frac{\sqrt{3}-1}{2}$t，
∵t2+3t2=4c2，∴t=c
∴e=$\frac{c}{a}$=$\sqrt{3}$+1
故选：D．
点评 本题主要考查了双曲线的简单性质．考查了学生对双曲线定义的理解和灵活运用．
练习册系列答案
相关题目
中，角
所对的边分别为
．若
，则角
等于（ ）
B．
C．
D．
5．定义在R上的偶函数f（x）满足f（x+1）=-f（x），且在[0，1]上单调递增，设a=f（3），b=f（$\sqrt{2}$），c=f（2），则a，b，c大小关系是（ ）
| A． | b＞c＞a | B． | a＞c＞b | C． | a＞b＞c | D． | c＞b＞a |
15．
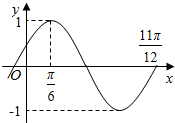设函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，为了得到函数y=cos2x的图象，只需将函数y=f（x）的图象（ ）
设函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，为了得到函数y=cos2x的图象，只需将函数y=f（x）的图象（ ）| A． | 向左平移$\frac{π}{6}$个单位 | B． | 向右平移$\frac{π}{6}$个单位 | ||
| C． | 向左平移$\frac{π}{3}$个单位 | D． | 向右平移$\frac{π}{3}$个单位 |