题目内容
4．f（x）是定义在R上的奇函数，f（-3）=2，则下列各点在函数f（x）图象上的是（ ）| A． | （3，-2） | B． | （3，2） | C． | （-3，-2） | D． | （2，-3） |
分析 根据f（x）是定义在R上的奇函数，f（-3）=2，可得：f（3）=-2，进而得到答案．
解答 解：∵f（x）是定义在R上的奇函数，f（-3）=2，
∴f（3）=-2，
故（3，-2）在函数f（x）图象上，
故选：A
点评 本题考查的知识点是函数奇偶性的性质，难度不大，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
15．
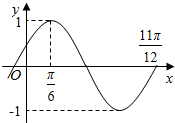设函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，为了得到函数y=cos2x的图象，只需将函数y=f（x）的图象（ ）
设函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，为了得到函数y=cos2x的图象，只需将函数y=f（x）的图象（ ）| A． | 向左平移$\frac{π}{6}$个单位 | B． | 向右平移$\frac{π}{6}$个单位 | ||
| C． | 向左平移$\frac{π}{3}$个单位 | D． | 向右平移$\frac{π}{3}$个单位 |
15．
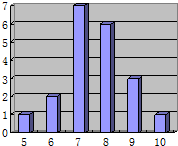某射击小组有20个人，教练根据他们某次射击的数据绘制成如图的统计图，则这组数据的众数和中位数分别是（ ）
某射击小组有20个人，教练根据他们某次射击的数据绘制成如图的统计图，则这组数据的众数和中位数分别是（ ）| A． | 7，7 | B． | 8，7.5 | C． | 7，7.5 | D． | 8，6 |
16．已知a＞0，b＜0，则“a+b=0”是“a+b≥2ab”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |