题目内容
3.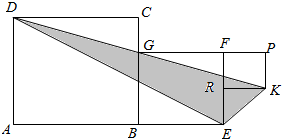 正方形ABCD、正方形BEFG和正方形RKPF的位置如图所示,点G在线段DK上,正方形BEFG的边长为4,则△DEK的面积为( )
正方形ABCD、正方形BEFG和正方形RKPF的位置如图所示,点G在线段DK上,正方形BEFG的边长为4,则△DEK的面积为( )| A. | 10 | B. | 12 | C. | 14 | D. | 16 |
分析 设FP=a,CG=x,由GP∥CD,点G在线段DK上,可得Rt△DCG∽Rt△GPK,可得x=a.设FM=y,由△MFG∽△MRK,可得y=$\frac{4a}{a+4}$.利用△DEK的面积S=S正方形ABCD+S矩形BNPG-S△DAE-2S△DCG-S△ENK,即可得出.
解答 解:设FP=a,CG=x,
∵GP∥CD,点G在线段DK上,∴Rt△DCG∽Rt△GPK,∴$\frac{x}{a}=\frac{4+x}{4+a}$,解得x=a.
设FM=y,由△MFG∽△MRK,可得$\frac{y}{a-y}=\frac{4}{a}$,可得y=$\frac{4a}{a+4}$.
∴△DEK的面积S=(4+a)2+4(4+a)-$\frac{1}{2}(4+a)(8+a)$-$2×\frac{1}{2}(4+a)a$-$\frac{1}{2}(4-a)a$=16.
故选:D.
点评 本题考查了正方形的性质、相似三角形的性质、直角三角形的面积,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.设等差数列{an}满足5a7=7a10,且a1>0,Sn为其前n项和,则Sn中最大的是( )
| A. | S16 | B. | S17 | C. | S18 | D. | S16或S17 |
15.-700°是( )角.
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
8.f(x)=ax3+3x2+2,若f′(-1)=7,则a的值等于( )
| A. | $\frac{19}{3}$ | B. | $\frac{16}{3}$ | C. | $\frac{13}{3}$ | D. | $\frac{10}{3}$ |
15.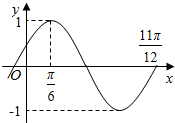 设函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,为了得到函数y=cos2x的图象,只需将函数y=f(x)的图象( )
设函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,为了得到函数y=cos2x的图象,只需将函数y=f(x)的图象( )
 设函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,为了得到函数y=cos2x的图象,只需将函数y=f(x)的图象( )
设函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,为了得到函数y=cos2x的图象,只需将函数y=f(x)的图象( )| A. | 向左平移$\frac{π}{6}$个单位 | B. | 向右平移$\frac{π}{6}$个单位 | ||
| C. | 向左平移$\frac{π}{3}$个单位 | D. | 向右平移$\frac{π}{3}$个单位 |
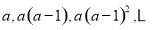 ,其前
,其前 项和为
项和为 .
.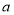 的取值范围及
的取值范围及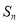 ;
;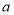 ,使
,使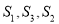 成等差数列?若存在,求出
成等差数列?若存在,求出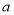 的值;若不存在,说明理由.
的值;若不存在,说明理由. 中,角
中,角 所对的边分别为
所对的边分别为 .若
.若 ,则角
,则角 等于( )
等于( ) B.
B. C.
C. D.
D.