题目内容
已知向量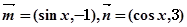
(1)当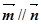 时,求
时,求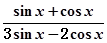 的值;
的值;
(2)设函数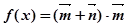 ,求
,求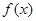 的单调增区间;
的单调增区间;
(3)已知在锐角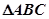 中,
中,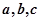 分别为角
分别为角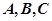 的对边,
的对边,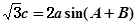 ,对于(2)中的函数
,对于(2)中的函数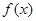 ,求
,求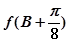 的取值范围。
的取值范围。
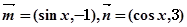
(1)当
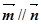 时,求
时,求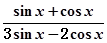 的值;
的值;(2)设函数
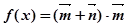 ,求
,求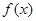 的单调增区间;
的单调增区间;(3)已知在锐角
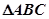 中,
中,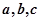 分别为角
分别为角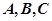 的对边,
的对边,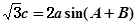 ,对于(2)中的函数
,对于(2)中的函数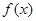 ,求
,求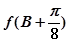 的取值范围。
的取值范围。(1)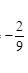 . (2)
. (2)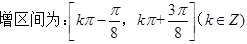 ,
,
(3)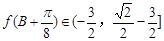 .
.
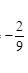 . (2)
. (2)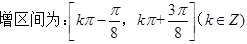 ,
,(3)
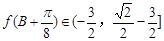 .
.试题分析:(1)由
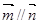 ,可得3sinx=-cosx,于是tanx=
,可得3sinx=-cosx,于是tanx=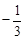 .
.∴
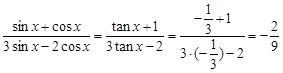 .
. (2)∵
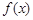 =
=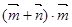
=(sinx+cosx,2)·(sinx,-1)
=sin2x+sinxcosx-2
=
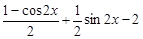
=
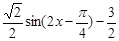 ,
, 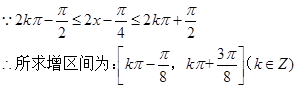
(无
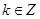 扣1分)
扣1分)(3)∵在△ABC中,A+B=
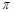 -C,于是
-C,于是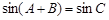 ,
,由正弦定理知:
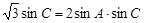 ,
,∴
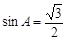 ,可解得
,可解得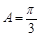 .
. 又△ABC为锐角三角形,于是
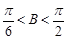 ,
,∴
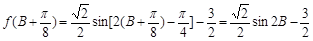 .
.由
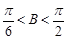 得
得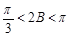 ,
,∴ 0<sin2B≤1,得
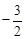 <
<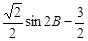 ≤
≤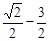 .
.即
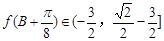 .
.点评:典型题,为研究三角函数的图象和性质,往往需要利用三角函数和差倍半公式将函数“化一”。本题由平面向量的坐标运算得到f(x)的表达式,通过“化一”,利用三角函数性质,求得周期、最小值。(3)则利用正弦定理,求得角A,进一步得到角B的范围,达到解题目的。

练习册系列答案
相关题目
 ,且
,且 与
与 夹角是锐角,则
夹角是锐角,则 的取值范围是____________.
的取值范围是____________. 与
与 的夹角为
的夹角为 ,
, ,则
,则 = ( )
= ( )

 ,满足
,满足 ,且
,且 ,
, ,则
,则 ( ).
( ).

 ,
,  ,如果向量
,如果向量 与
与 垂直,则
垂直,则 的值为( )
的值为( )


 中,若
中,若 ,则
,则 ;②已知
;②已知 ,则
,则 在
在 上的投影为
上的投影为 ;③已知
;③已知 ,
, ,则“
,则“ ”为假命题.其中真命题的个数为( )
”为假命题.其中真命题的个数为( ) ,
,
 ,且
,且 ∥(
∥( ),求x的值;
),求x的值; ,求实数
,求实数 的取值范围.
的取值范围. 是单位向量,若向量
是单位向量,若向量 满足
满足 ,则
,则 的取值范围是 .
的取值范围是 .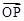 的坐标为______.
的坐标为______.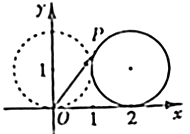
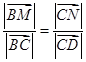 ,则
,则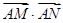 的取值范围是________.
的取值范围是________.