题目内容
设△ABC的三个内角A、B、C所对的边长依次为a、b、c,若△ABC的面积为S,且S=a2-(b-c)2,则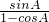 =________.
=________.
4
分析:根据S=a2-(b-c)2 = bc•sinA,把余弦定理代入化简可得4-4cosA=sinA,由此求得
bc•sinA,把余弦定理代入化简可得4-4cosA=sinA,由此求得 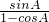 的值.
的值.
解答:∵△ABC的面积为S,且S=a2-(b-c)2 =a2-b2-c2+2bc= bc•sinA,
bc•sinA,
∴由余弦定理可得-2bc•cosA+2bc= bc•sinA,
bc•sinA,
∴4-4cosA=sinA,
∴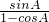 =
= =4,
=4,
故答案为 4.
点评:本题主要考查三角形的面积公式,余弦定理的应用,属于中档题.
分析:根据S=a2-(b-c)2 =
 bc•sinA,把余弦定理代入化简可得4-4cosA=sinA,由此求得
bc•sinA,把余弦定理代入化简可得4-4cosA=sinA,由此求得 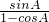 的值.
的值.解答:∵△ABC的面积为S,且S=a2-(b-c)2 =a2-b2-c2+2bc=
 bc•sinA,
bc•sinA,∴由余弦定理可得-2bc•cosA+2bc=
 bc•sinA,
bc•sinA,∴4-4cosA=sinA,
∴
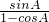 =
= =4,
=4,故答案为 4.
点评:本题主要考查三角形的面积公式,余弦定理的应用,属于中档题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目