题目内容
【题目】在直角坐标系xOy中,曲线C1: ![]() (t为参数,t ≠ 0),其中0 ≤ α < π,在以O为极点,x轴正半轴为极轴的极坐标系中,曲线C2:
(t为参数,t ≠ 0),其中0 ≤ α < π,在以O为极点,x轴正半轴为极轴的极坐标系中,曲线C2: ![]() ,C3:
,C3: ![]() .
.
(1)求C2与C3交点的直角坐标;
(2)若C1与C2相交于点A,C1与C3相交于点B,求 ![]() 的最大值.
的最大值.
【答案】
(1)解:曲线 ![]() 的直角坐标方程为
的直角坐标方程为 ![]() ,
,
曲线 ![]() 的直角坐标方程为
的直角坐标方程为 ![]() .
.
联立 ![]() 解得
解得 ![]() 或
或 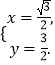
所以 ![]() 与
与 ![]() 交点的直角坐标为
交点的直角坐标为 ![]() 和
和 ![]()
(2)解:曲线 ![]() 的极坐标方程为
的极坐标方程为 ![]() ,其中
,其中 ![]()
因此 ![]() 的极坐标为
的极坐标为 ![]() ,
, ![]() 的极坐标为
的极坐标为 ![]()
所以 ![]()
当 ![]() 时,
时, ![]() 取得最大值,最大值为4
取得最大值,最大值为4
【解析】(1)将C2与C3转化为直角坐标方程,解方程组即可求出交点坐标;(2)求出A,B的极坐标,利用距离公式进行求解.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目