题目内容
【题目】在![]() 中,
中,![]() ,
,![]() 是
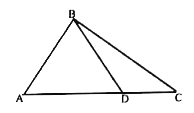
是![]() 上一点,
上一点,![]() ,且
,且![]() ,则
,则![]() __________.
__________.
【答案】-4
【解析】分析:先利用同角三角的基本关系求得sinC和sin∠DBC的值,结合∠BDA=C+∠DBC,利用两角和的余弦公式求得 cos∠BDA 的值,可得∠BDA 的值.
再求出△ABC中各边的长,再由D是AC上一点,![]() ,我们将相关数据代入平面向量数量积公式即可求解.
,我们将相关数据代入平面向量数量积公式即可求解.
详解:△ABC中,∵cosC=![]() ,cos∠DBC=
,cos∠DBC=![]() ,
,
∴sinC=![]() ,sin∠DBC=
,sin∠DBC=![]() ,
,
∵∠BDC=π﹣C﹣∠DBC,
∴∠BDA=C+∠DBC,
∴cos∠BDA=cos(C+∠DBC )=cosCcos∠DBC﹣sinCsin∠DBC
=![]() ×
×![]() ﹣
﹣![]() =
=![]() ,
,
∴∠BDA=![]() .
.
设DC=x,BC=a,
在△BDC中,由正弦定理得![]() ,
,
∴a=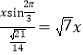 ,
,
在△ABC中,AC=3x,BC=![]() ,AB=2,
,AB=2,
∴cosC=![]() =
=![]() ,解得x=1,∴AD=2,CB=
,解得x=1,∴AD=2,CB=![]() ,
,
∴![]() =2
=2![]() cos(π﹣C)=2
cos(π﹣C)=2![]() (﹣cosC)=﹣2
(﹣cosC)=﹣2![]()
![]() =﹣4.
=﹣4.
故填-4.

练习册系列答案
相关题目