题目内容
【题目】在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,![]() =2
=2![]() =2.
=2.
(1)求证:![]() ;
;
(2)求证:![]() ∥平面
∥平面![]() ;
;
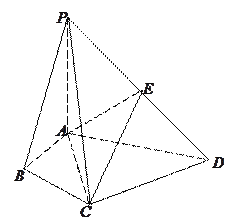
【答案】(1)见解析(2)见解析
【解析】分析:(1)取PC中点F,利用等腰三角形的性质可得PC⊥AF,先证明CD⊥平面PAC,可得CD⊥PC,从而EF⊥PC,故有PC⊥平面AEF,进而证得PC⊥AE.
(2)取AD中点M,利用三角形的中位线证明EM∥平面PAB,利用同位角相等证明MC∥AB,得到平面EMC∥平面PAB,证得EC∥平面PAB.
详解:(1)在Rt△ABC中,AB=1,∠BAC=60°,
∴BC=![]() ,AC=2.取
,AC=2.取![]() 中点
中点![]() ,连AF, EF,
,连AF, EF,
∵PA=AC=2,∴PC⊥![]() .
.
∵PA⊥平面ABCD,![]() 平面ABCD,
平面ABCD,
∴PA⊥![]() ,又∠ACD=90°,即
,又∠ACD=90°,即![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴![]() .
.
∴![]() .
.
∴PC⊥![]() .
.
(2)证法一:取AD中点M,连EM,CM.则
EM∥PA.∵EM ![]() 平面PAB,PA
平面PAB,PA![]() 平面PAB,
平面PAB,
∴EM∥平面PAB.
在Rt△ACD中,∠CAD=60°,AC=AM=2,
∴∠ACM=60°.而∠BAC=60°,∴MC∥AB.
∵MC ![]() 平面PAB,AB
平面PAB,AB![]() 平面PAB,
平面PAB,
∴MC∥平面PAB.
∵EM∩MC=M,∴平面EMC∥平面PAB.
∵EC![]() 平面EMC,∴EC∥平面PAB.
平面EMC,∴EC∥平面PAB.
证法二:延长DC、AB,设它们交于点N,连PN.
∵∠NAC=∠DAC=60°,AC⊥CD,∴C为ND的中点
∵E为PD中点,∴EC∥PN
∵EC ![]() 平面PAB,PN
平面PAB,PN![]() 平面PAB,∴EC∥平面PAB.
平面PAB,∴EC∥平面PAB.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目