题目内容
15．已知集合A={与$\overrightarrow{a}$共线的向量}，B={与$\overrightarrow{a}$长度相等的向量}，C={与$\overrightarrow{a}$长度相等、方向相反的向量}，其中$\overrightarrow{a}$为非零向量，则A∩C⊆B（填“⊆”或“?”）分析 利用共线向量的定义：方向相同或相反的向量；判断出各个集合的关系．
解答 解：与共线的向量是与其方向相同或相反的向量，
∵集合A={与$\overrightarrow{a}$共线的向量}，C={与$\overrightarrow{a}$长度相等、方向相反的向量}，
∴A∩C=C，
∵与$\overrightarrow{a}$长度相等的向量，方向任意，故C⊆B，
∴C⊆B，
故A∩C⊆B
故答案为：⊆．
点评 本题考查向量共线的定义：方向相同或相反的向量．
练习册系列答案
相关题目
3．为了得到函数y=sin（-3x）的图象，只需将函数y=cos（3x+$\frac{π}{4}$）的图象（ ）
| A． | 向左平移$\frac{π}{4}$个单位 | B． | 向右平移$\frac{π}{4}$个单位 | ||
| C． | 向左平移$\frac{π}{12}$个单位 | D． | 向右平移$\frac{π}{12}$个单位 |
=（2cosωx,-1）,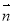
=（sinωx-cosωx,2）（ ω>0），函数f（x）= 
.
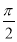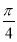个单位，然后纵坐标不变，横坐标缩短为原来的
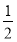倍，得到函数g（x）的图象，当x∈[
,
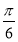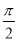]时，求函数g（x）的值域.