题目内容
2.设f(x)的定义域为(1,3),则函数f(x2)的定义域是($-\sqrt{3}$,-1)∪(1,$\sqrt{3}$).分析 直接由x2大于1小于3,求解不等式即可得答案.
解答 解:由1<x2<3,
得$-\sqrt{3}<x<-1$或$1<x<\sqrt{3}$,
∴函数f(x2)的定义域是:($-\sqrt{3}$,-1)∪(1,$\sqrt{3}$).
故答案为:($-\sqrt{3}$,-1)∪(1,$\sqrt{3}$).
点评 本题考查了函数的定义域及其求法,考查了不等式的解法,是基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10. 如图所示,在棱长为a的正方体ABCD-A1B1C1D1的面对角线A1B上存在一点P使得AP+D1P取得最小值,若此最小值为$2\sqrt{2+\sqrt{2}}$,则a的值是( )
如图所示,在棱长为a的正方体ABCD-A1B1C1D1的面对角线A1B上存在一点P使得AP+D1P取得最小值,若此最小值为$2\sqrt{2+\sqrt{2}}$,则a的值是( )
 如图所示,在棱长为a的正方体ABCD-A1B1C1D1的面对角线A1B上存在一点P使得AP+D1P取得最小值,若此最小值为$2\sqrt{2+\sqrt{2}}$,则a的值是( )
如图所示,在棱长为a的正方体ABCD-A1B1C1D1的面对角线A1B上存在一点P使得AP+D1P取得最小值,若此最小值为$2\sqrt{2+\sqrt{2}}$,则a的值是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
17.设f(x)与g(x)是定义在同一区间[a,b]上的两个函数,若函数y=f(x)-g(x)在x∈[a,b]上有两个不同的零点,则称f(x)和g(x)在[a,b]上是“关联函数”,区间[a,b]称为“关联区间”.若f(x)=x2-3x+1与g(x)=x+m在[0,3]上是“关联函数”,则m的取值范围为( )
| A. | (-3,+∞) | B. | (-3,-2] | C. | [-3,0] | D. | [-2,1] |
12.已知集合A={-1,1},B={1,2},则A∪B=( )
| A. | ∅ | B. | {-1,1} | C. | {1,2} | D. | {-1,1,2} |
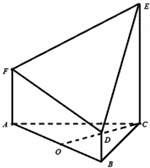 如图所示的几何体是由等边三角形ABC的底面的棱柱被平面DEF所截得,已知FA⊥平面ABC,AB=2,BD=1,AF=2,CE=3,O为AB的中点.
如图所示的几何体是由等边三角形ABC的底面的棱柱被平面DEF所截得,已知FA⊥平面ABC,AB=2,BD=1,AF=2,CE=3,O为AB的中点.