��Ŀ����
10������У���е�ѡ�ν�ҵ�����У�����ѡ�ޡ���ѧ��������ͬѧ��ͬʱҲѡ���ˡ��Ķ������Ŀγ̣�ѡ�ޡ��Ķ�������ͬѧ��ͬʱҲѡ���ˡ���ѧ�������Ŀγ̣�ѡ�ν�ҵ�ɼ���ΪA��B��C��D��E����ȼ���ij�������������ƿ��Գɼ�������ͳ����ͼ��ʾ�����С���ѧ��������Ŀ�ijɼ�ΪB�Ŀ�����10�ˣ�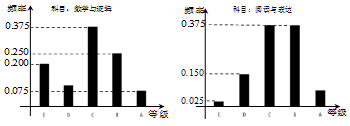
��1����ÿ��������С��Ķ�������Ŀ�гɼ�ΪA��������
��2�����ڴӡ���ѧ��������Ŀ�ijɼ�ΪA��D�Ŀ����������ȡ���ˣ�����鵽�������������dzɼ�ΪA�Ŀ����ĸ��ʣ�
���� ��1�����ݡ���ѧ��������Ŀ�ijɼ�ΪB�Ŀ�����10�ˣ������������=Ƶ����Ƶ�ʵó��ÿ��������������Ӷ��õ��ÿ��������С��Ķ�������Ŀ�гɼ��ȼ�ΪA��������
��2��ͨ���оٵķ��������ѡ����2�����п��ܵ�����������˵����Ƴɼ��ȼ���ΪA����������ùŵ�����ʹ�ʽ��������ȡ���˽��з�̸�������˵����Ƴɼ��ȼ���ΪA�ĸ��ʣ�
��� �⣺��1����Ϊ����ѧ��������Ŀ�гɼ��ȼ�ΪB�Ŀ�����10�ˣ�
���Ըÿ�����10��0.25=40�ˣ�����2�֣�
���Ըÿ��������С��Ķ�������Ŀ�гɼ��ȼ�ΪA������Ϊ40����1-0.375-0.375-0.15-0.025��=3 �ˣ� ����4�֣�
��2����Ϊ����ѧ��������Ŀ�гɼ��ȼ�ΪB�Ŀ�����10�ˣ����Ըÿ�����10��0.25=40�ˣ���ɼ�ΪA�Ŀ�����40��0.075=3�ˣ�����6�֣�
�ɼ�ΪD�Ŀ�����40����1-0.2-0.375-0.25-0.075��=4�� ����8�֣�
��ɼ�ΪA�Ŀ���Ϊa��b��c���ɼ�ΪD�Ŀ���Ϊd��e��f��g��
�����ȡ���˽��з�̸�������¼�����21�����ֱ�Ϊ��a��b����a��c����a��d����a��e����a��f����a��g����b��c����b��d����b��e����b��f����b��g����c��d����c��e����c��f����c��g����d��e����d��f����d��g����e��f����e��g����f��g��
���¼�N���鵽�������������dzɼ�ΪA�Ŀ���������10�֣�
���¼�N������a��b����a��c����b��c����
��$P��N��=\frac{3}{21}=\frac{1}{7}$����12�֣�
���� ��С����Ҫ����ͳ������ʵ����֪ʶ�������漰��Ƶ�ʷֲ�ֱ��ͼ���ŵ���͵����ݣ����ڻ����⣮

 ����С��ʿ���������ϵ�д�
����С��ʿ���������ϵ�д�| A�� | sin$\frac{19��}{8}$��cos$\frac{14��}{9}$ | B�� | sin��-$\frac{54��}{7}$����sin��-$\frac{63��}{8}$�� | ||
| C�� | tan��-$\frac{13��}{4}$����tan��-$\frac{17��}{5}$�� | D�� | tan138�㣾tan143�� |
| A�� | $\sqrt{2}$ | B�� | $\sqrt{3}$ | C�� | 2 | D�� | $\sqrt{5}$ |
| A�� | 12 | B�� | 14 | C�� | 3 | D�� | 21 |
| A�� | -39 | B�� | 5 | C�� | 39 | D�� | 65 |
| �� �� | 1��10�� | 2��10�� | 3��10�� | 4��10�� | 5��10�� | 6��10�� |
| ��ҹ�²�x����C�� | 10 | 11 | 13 | 12 | 8 | 6 |
| ��������y������ | 22 | 25 | 29 | 26 | 16 | 12 |
��1����ѡȡ��2������ǡ�������������µĸ��ʣ�
��2����ѡȡ����1����6�µ��������ݣ������2��5�·ݵ����ݣ����y����x�����Իع鷽��y=bx+a��
������$\widehat{b}$=$\frac{\sum_{i=1}^{n}��{x}_{i}-\overline{x}����{y}_{i}-\overline{y}��}{\sum_{i=1}^{n}��{x}_{i}-\overline{x}��^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$��
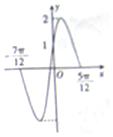
| A�� | -1 | B�� | 1 | C�� | -$\frac{1}{2}$ | D�� | $\frac{1}{2}$ |
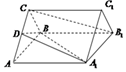 ��ͼ����������ABC-A1B1C1�ĵ���߳���2�����ⳤ��$\sqrt{3}$��D��AC���е㣮
��ͼ����������ABC-A1B1C1�ĵ���߳���2�����ⳤ��$\sqrt{3}$��D��AC���е㣮