题目内容
2.已知O为直角坐标原点,点A(2,3),点P为平面区域$\left\{\begin{array}{l}{x+1≥0}\\{x+y≤2}\\{y≥m(x-2)}\end{array}\right.$(m>0)内的一动点,若$\overrightarrow{OA}$•$\overrightarrow{OP}$的最小值为-6,则m=( )| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{4}{9}$ | D. | $\frac{1}{3}$ |
分析 根据向量数量积的公式求出$\overrightarrow{OA}$•$\overrightarrow{OP}$=2x+3y,结合$\overrightarrow{OA}$•$\overrightarrow{OP}$的最小值为-6,得到y=-$\frac{2}{3}$x-2,作出对应的直线方程,求出交点坐标进行求解即可.
解答 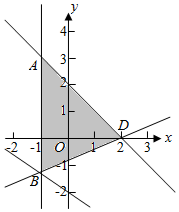 解:∵$\overrightarrow{OA}$•$\overrightarrow{OP}$=2x+3y,
解:∵$\overrightarrow{OA}$•$\overrightarrow{OP}$=2x+3y,
∴设z=2x+3y,得y=$-\frac{2}{3}x+\frac{z}{3}$,
∵$\overrightarrow{OA}$•$\overrightarrow{OP}$的最小值为-6,
∴此时y=-$\frac{2}{3}$x-2,
作出y=-$\frac{2}{3}$x-2则y=-$\frac{2}{3}$x-2与x=-1相交为B时,
此时B(-1,-$\frac{4}{3}$),此时B也在y=m(x-2)上,
则-3m=-$\frac{4}{3}$,得m=$\frac{4}{9}$,
故选:C.
点评 本题主要考查线性规划的应用,利用数量积的公式求出目标函数的解析式,先作出目标函数的直线,求出交点坐标是解决本题的关键.

练习册系列答案
相关题目
7.$\frac{sin87°-cos63°cos60°}{cos27°}$等于( )
| A. | -$\frac{\sqrt{3}}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |