题目内容
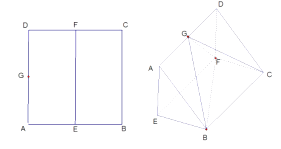
【题目】如图, ![]() ,
, ![]() ,
, ![]() 分别是
分别是 ![]() 的中点,将
的中点,将 ![]() 沿直线
沿直线 ![]() 折起,使二面角
折起,使二面角 ![]() 的大小为
的大小为 ![]() ,则
,则 ![]() 与平面
与平面 ![]() 所成角的正切值是( )
所成角的正切值是( )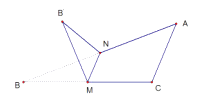
A.![]()
B.![]()
C.![]()
D.![]()
【答案】D
【解析】∵ ![]() ,AC=BC,M、N分别是BC、AB的中点,
,AC=BC,M、N分别是BC、AB的中点,
将△BMN沿直线MN折起,使二面角B′﹣MN﹣B的大小为 ![]() ,
,
∴∠BMB′为二面角 ![]() 的平面角,即∠BMB′=
的平面角,即∠BMB′= ![]() ,
,
取BM的中点D,连B′D,ND,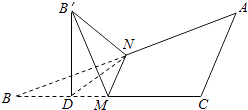
由题意易知:折叠之后平面B′MN与平面BMN所成的二面角即为∠B′MD=60°,
并且B′在底面ACB内的投影点D就在BC上,且恰在BM的中点位置,
∴B′D⊥BC,B′D⊥AD,B′D⊥面ABC,
∴∠B′ND就为斜线B′N与平面ABC所成的角
设AC=BC=t,则B′D= ![]() ,B′N=
,B′N= ![]() ,DN=
,DN= ![]() ,
,
tan∠B′ND= ![]() =
= ![]() .
.
故B'N与平面ABC所成角的正切值是 ![]() .
.
所以答案是:D.
【考点精析】利用空间角的异面直线所成的角对题目进行判断即可得到答案,需要熟知已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则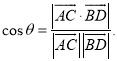 .
.

练习册系列答案
相关题目