题目内容
【题目】已知函数![]() ,
,![]() .
.
(Ⅰ)若![]() ,解不等式
,解不等式![]() ;
;
(Ⅱ)若不等式![]() 至少有一个负数解,求实数
至少有一个负数解,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ){x|1≤x≤0}.(Ⅱ)(![]()
![]() ,2).
,2).
【解析】【试题分析】(I)当![]() 时,利用零点分段法去绝对值,将不等式变为分段不等式来求得解集.(II)作出函数
时,利用零点分段法去绝对值,将不等式变为分段不等式来求得解集.(II)作出函数![]() 的图象和函数
的图象和函数![]() 的图象,通过数形结合与分类讨论的数学思想方法求得
的图象,通过数形结合与分类讨论的数学思想方法求得![]() 的取值范围.
的取值范围.
【试题解析】
(Ⅰ)若a=1,则不等式![]() +
+![]() ≥3化为2
≥3化为2![]() +|x1|≥3.
+|x1|≥3.
当x≥1时,2![]() +x1≥3,即
+x1≥3,即![]() x+2≤0,(x
x+2≤0,(x![]()
![]() )2+
)2+![]()
![]() ≤0不成立;
≤0不成立;
当x<1时,2![]() x+1≥3,即
x+1≥3,即![]() +x≤0,解得1≤x≤0.
+x≤0,解得1≤x≤0.
综上,不等式![]() +
+![]() ≥3的解集为{x|1≤x≤0}.
≥3的解集为{x|1≤x≤0}.
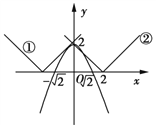
(Ⅱ)作出y=![]() 的图象如图所示,当a<0时,
的图象如图所示,当a<0时,![]() 的图象如折线①所示,
的图象如折线①所示,
由![]() ,
,![]() 得
得![]() +xa2=0,若相切,则Δ=1+4(a+2)=0,得a=
+xa2=0,若相切,则Δ=1+4(a+2)=0,得a=![]()
![]() ,
,
数形结合知,当a≤![]()
![]() 时,不等式无负数解,则
时,不等式无负数解,则![]()
![]() <a<0.
<a<0.
当a=0时,满足![]() >
>![]() 至少有一个负数解.
至少有一个负数解.
当a>0时,![]() 的图象如折线②所示,
的图象如折线②所示,
此时当a=2时恰好无负数解,数形结合知,
当a≥2时,不等式无负数解,则0<a<2.
综上所述,若不等式![]() >
>![]() 至少有一个负数解,
至少有一个负数解,
则实数a的取值范围是(![]()
![]() ,2).
,2).

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某品牌汽车的![]() 店,对最近100份分期付款购车情况进行统计,统计情况如下表所示.已知分9期付款的频率为0.4;该店经销一辆该品牌汽车,若顾客分3期付款,其利润为1万元;分6期或9期付款,其利润为2万元;分12期付款,其利润为3万元.
店,对最近100份分期付款购车情况进行统计,统计情况如下表所示.已知分9期付款的频率为0.4;该店经销一辆该品牌汽车,若顾客分3期付款,其利润为1万元;分6期或9期付款,其利润为2万元;分12期付款,其利润为3万元.
付款方式 | 分3期 | 分6期 | 分9期 | 分12期 |
频数 | 20 | 20 |
|
|
(1)若以上表计算出的频率近似替代概率,从该店采用分期付款购车的顾客(数量较大)中随机抽取3为顾客,求事件![]() :“至多有1位采用分6期付款“的概率
:“至多有1位采用分6期付款“的概率![]() ;
;
(2)按分层抽样方式从这100为顾客中抽取5人,再从抽取的5人中随机抽取3人,记该店在这3人身上赚取的总利润为随机变量![]() ,求
,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
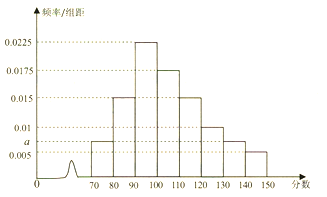
【题目】中央政府为了应对因人口老龄化而造成的劳动力短缺等问题,拟定出台“延迟退休年龄政策”.为了了解人们对“延迟退休年龄政策”的态度,责成人社部进行调研.人社部从网上年龄在15~65岁的人群中随机调查100人,调查数据的频率分布直方图如图所示, 支持“延迟退休年龄政策”的人数与年龄的统计结果如表:

年龄(岁) |
|
|
|
|
|
支持“延迟退休年龄政策”人数 | 15 | 5 | 15 | 28 | 17 |
(I)由以上统计数据填写下面的![]() 列联表;
列联表;
年龄低于45岁的人数 | 年龄不低于45岁的人数 | 总计 | |
支持 | |||
不支持 | |||
总计 |
(II)通过计算判断是否有![]() 的把握认为以45岁为分界点的不同人群对“延迟退休年龄政策”的态度有差异.
的把握认为以45岁为分界点的不同人群对“延迟退休年龄政策”的态度有差异.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
参考公式:![]()