题目内容
抛物线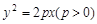 上纵坐标为
上纵坐标为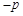 的点
的点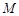 到焦点的距离为2.
到焦点的距离为2.
(Ⅰ)求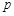 的值;
的值;
(Ⅱ)如图,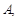
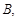
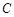 为抛物线上三点,且线段
为抛物线上三点,且线段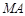 ,
,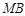 ,
,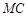 与
与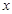 轴交点的横坐标依次组成公差为1的等差数列,若
轴交点的横坐标依次组成公差为1的等差数列,若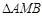 的面积是
的面积是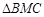 面积的
面积的 ,求直线
,求直线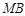 的方程.
的方程.

(本题15分):(Ⅰ)解:设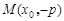 ,
则
,
则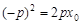 ,
,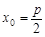 ,
,
由抛物线定义,得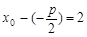 所以
所以 .
……5分
.
……5分
(Ⅱ)由(Ⅰ)知抛物线方程为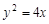 ,
,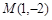 .
.
设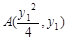 ,
,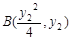 ,
,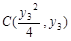 (
(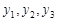 均大于零) ……6分
均大于零) ……6分
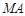 ,
,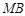 ,
,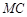 与
与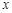 轴交点的横坐标依次为
轴交点的横坐标依次为 .
.
(1)当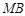
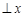 轴时,直线
轴时,直线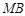 的方程为
的方程为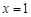 ,则
,则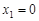 ,不合题意,舍去.
,不合题意,舍去.
……7分
(2)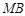 与
与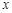 轴不垂直时,
轴不垂直时,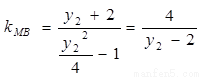 ,
,
设直线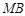 的方程为
的方程为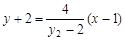 ,即
,即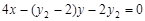 ,
,
令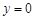 得2
得2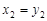 ,同理2
,同理2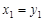 ,2
,2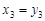 ,
……10分
,
……10分
因为 依次组成公差为1的等差数列,
依次组成公差为1的等差数列,
所以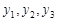 组成公差为2的等差数列. ……12分
组成公差为2的等差数列. ……12分
设点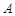 到直线
到直线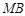 的距离为
的距离为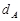 ,点
,点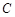 到直线
到直线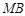 的距离为
的距离为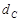 ,
,
因为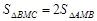 ,所以
,所以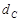 =2
=2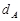 ,
,
所以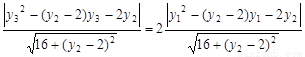 ……14分
……14分
得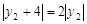 ,即
,即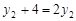 ,所以
,所以 ,
,
所以直线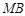 的方程为:
的方程为: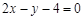 ……15分
……15分
解法二:(Ⅰ)同上.
(Ⅱ)由(Ⅰ)知抛物线方程为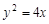 ,
,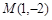 .
.
由题意,设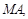
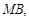
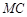 与
与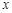 轴交点的横坐标依次为
轴交点的横坐标依次为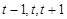
设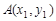 ,
,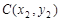 (
(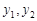 均大于零).
……6分
均大于零).
……6分
(1)当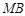
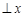 轴时,直线
轴时,直线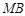 的方程为
的方程为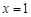 ,则
,则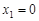 ,不合题意,舍去.
,不合题意,舍去.
……7分
(2)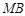 与
与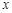 轴不垂直时,
轴不垂直时,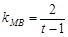
设直线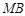 的方程为
的方程为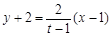 ,即
,即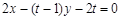 ,
,
同理直线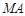 的方程为
的方程为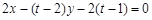 ,
,
由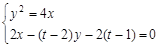 得
得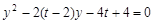
则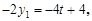 所以
所以 ,
……12分
,
……12分
同理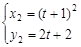 ,设点
,设点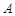 到直线
到直线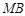 的距离为
的距离为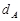 ,点
,点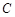 到直线
到直线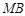 的距离为
的距离为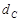 , 因为
, 因为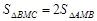 ,所以
,所以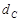 =2
=2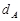 ,
,
所以 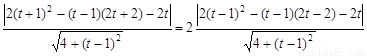 ……14分
……14分
化简得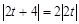 ,即
,即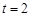 ,
,
所以直线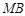 的方程为:
的方程为: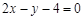 ……15分
……15分
【解析】略

 名校课堂系列答案
名校课堂系列答案
 的点到其焦点F的距离
的点到其焦点F的距离 的值,并证明直线AB的斜率是非零常数.
的值,并证明直线AB的斜率是非零常数.