题目内容
过抛物线y2=2px(p>0)上一定点P(x0,y0)(y0>0)作两条直线分别交抛物线于A(x1,y1)、B(x2,y2).
(1)求该抛物线上纵坐标为![]() 的点到其焦点F的距离;
的点到其焦点F的距离;
(2)当PA与PB的斜率存在且倾斜角互补时,求![]() 的值,并证明直线AB的斜率是非零常数.
的值,并证明直线AB的斜率是非零常数.
(1) 点M(![]() ,
,![]() )到F的距离为
)到F的距离为![]() -(-
-(-![]() )=
)=![]() .
.
(2)证明见解析
解析:
(1)当y=![]() 时,x=
时,x=![]() .
.
又抛物线y2=2px(p>0)的准线方程为x=-![]() ,
,
则点M(![]() ,
,![]() )到F的距离为
)到F的距离为![]() -(-
-(-![]() )=
)=![]() .
.
(2)设直线PA的斜率为kPA,直线PB的斜率为kPB.
由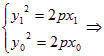 y12-y02=2p(x1-x0),
y12-y02=2p(x1-x0),
则kPA=![]() (x1≠x0).
(x1≠x0).
同理,得kPB=![]() (x2≠x0).
(x2≠x0).
由PA、PB的倾斜角互补知kPA=-kPB,
即![]() =-
=-![]() ,
,
即y1+y2=-2y0,故![]() =-2.
=-2.
设直线AB的斜率为kAB.
由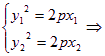 y12-y22=2p(x1-x2),
y12-y22=2p(x1-x2),
∴kAB=![]() (x1≠x2).
(x1≠x2).
将y1+y2=-2y0(y0>0)代入上式得
kAB=![]() .(P(x0,y0)为一定点,y0>0)
.(P(x0,y0)为一定点,y0>0)
则kAB=-![]() 为非零常数.
为非零常数.

练习册系列答案
相关题目
过抛物线y2=2px(p>0)的焦点F的直线l与抛物线在第一象限的交点为A,与抛物线的准线的交点为B,点A在抛物线准线上的射影为C,若
=
,
•
=48,则抛物线的方程为( )
| AF |
| FB |
| BA |
| BC |
| A、y2=4x | ||
| B、y2=8x | ||
| C、y2=16x | ||
D、y2=4
|
过抛物线y2=2px(p>0)的焦点F作直线交抛物线于A、B两点,O为抛物线的顶点.则△ABO是一个( )
| A、等边三角形 | B、直角三角形 | C、不等边锐角三角形 | D、钝角三角形 |