题目内容
过抛物线
上一定点
，作直线分别交抛物线于
（1）求该抛物线上纵坐标为
的点到焦点
的距离；
（2）当
与
的斜率存在且倾斜角互补时，求
的值，并证明直线
的斜率是非零常数。
解析:
（1）当
时，
，又抛物线的准线方程为
由抛物线的定义得，所求距离为
（2）设直线
的斜率为
，
的斜率为
，
由
，
，得
，同理
由于与的斜率存在且倾斜角互补，因此
即
，那么
再设
的斜率为
，同上即得
，将得
，显然，是非零常数。
练习册系列答案
全能测控期末小状元系列答案
相关题目
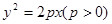上一定点
，作两条直线分别交抛物线于
，（1）求该抛物线上纵坐标为
的点到其焦点
的距离；（2）当
与
的斜率存在且倾斜角互补时，求
的值，并证明直线
的斜率是非零常数。
上一定点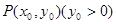
，作两条直线分别交抛物线于
、
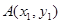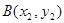．当
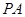与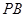
的斜率存在且倾斜角互补时，则
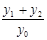的值为（ ）
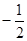B.
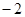C.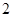
D.无法确定
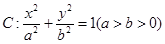的离心率为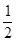
，
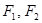为椭圆的左右焦点，
；
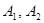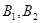分别为椭圆的长轴和短轴的端点(如图) . 若四边形
的面积为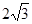
.
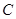的方程.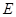
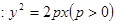的焦点与椭圆
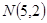任意作一条直线
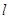，交抛物线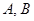
两点. 证明：以
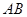为直径的所有圆是否过抛物线
上一定点
作两条直线分别交抛物线于
，
，
的点到焦点的距离为1，求抛物线方程；
，试证明：过
、
两点的直线必过定点
；
与
的斜率存在且倾斜角互补时，求
的值，并证明直线
的斜率是非零常数。